Other Schemes (unclassified) - structured grids

From CFD-Wiki

(Difference between revisions)

Jump to: navigation, search

Latest revision as of 21:09, 10 December 2010

Chakravarthy-Osher limiter

Sweby 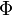$\Phi$ - limiter

Superbee limiter

R-k limiter

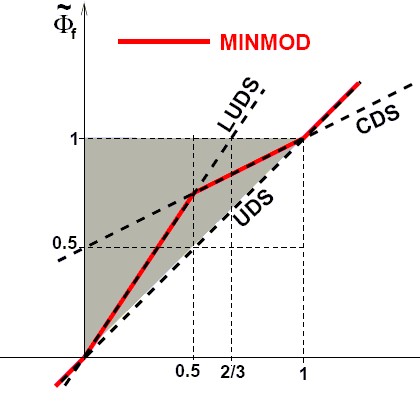
MINMOD - MINimum MODulus

Harten A. High resolution schemes using flux limiters for hyperbolic conservation laws. Journal of Computational Physics 1983; 49: 357-393

A. Harten

High Resolution Schemes for Hyperbolic Conservation Laws

J. Comp. Phys., vol. 49, no. 3, pp. 225-232, 1991

Identical to SOUCUP

Normalized variables - uniform grids

$\hat{\phi_{f}}= \begin{cases} \frac{3}{2} \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq \frac{1}{2} \\ \frac{1}{2} + \frac{1}{2} \hat{\phi_{C}} & \frac{1}{2} \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

Normalized variables - non-uniform grids (NVSF)

$\hat{\phi_{f}}= \begin{cases} \frac{\hat{\xi}_f}{\hat{\xi}_C} \hat{\phi}_C & 0 \leq \hat{\phi_{C}} \leq \hat{\xi}_C \\ \frac{ 1 - \hat{\xi}_f }{ 1 - \hat{\xi}_C } \hat{\phi}_C + \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } & \hat{\xi}_C \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

SOUCUP - Second-Order Upwind Central differnce-first order UPwind

Zhu J. (1992), "On the higher-order bounded discretization schemes for finite volume computations of incompressible flows", Computational Methods in Applied Mechanics and Engineering. 98. 345-360.

J. Zhu, W.Rodi (1991), "A low dispersion and bounded convection scheme", Comp. Meth. Appl. Mech.&Engng, Vol. 92, p 225.

Normalized variables - uniform grids

$\hat{\phi_{f}}= \begin{cases} \frac{3}{2} \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq \frac{1}{2} \\ \frac{1}{2} + \frac{1}{2} \hat{\phi_{C}} & \frac{1}{2} \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

Normalized variables - non-uniform grids

$\hat{\phi_{f}}= \begin{cases} a_{f}+ b_{f} \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq x_{Q} \\ c_{f}+ d_{f} \hat{\phi_{C}} & x_{Q} \leq \hat{\phi_{C}}\leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

where

$\boldsymbol{a_{f}= 0}$

(2)

$\boldsymbol{b_{f}= y_{Q}/x_{Q} }$

(2)

$c_{f}= \left( x_{Q} - y_{Q} \right)/\left( 1 - x_{Q} \right)$

(2)

$d_{f} = \left( 1 - y_{Q} \right) / \left( 1 - x_{Q} \right)$

(2)

ISNAS - Interpolation Scheme which is Nonoscillatory for Advected Scalars

Third-order flux-limiter scheme

M. Zijlema , On the construction of a third-order accurate monotone convection scheme with application to turbulent flows in general domains. International Journal for numerical methods in fluids, 22:619-641, 1996.

COPLA - COmbination of Piecewise Linear Approximation

Seok Ki Choi, Ho Yun Nam, Mann Cho

Evaluation of a High-Order Bounded Convection Scheme: Three-Dimensional Numerical Experiments

Numerical Heat Transfer, Part B, 28:23-38, 1995

$\hat{\phi}_{f}= \begin{cases} a_{f} + b_{f} \hat{\phi}_{C} & 0 \leq \hat{\phi}_{C} \leq 0.5 x_Q \\ c_{f} + d_{f} \hat{\phi}_{C} & 0.5 x_Q \leq \hat{\phi}_{C} \leq 1.5 x_Q\\ e_{f} + f_{f} \hat{\phi}_{C} & 1.5 x_Q \leq \hat{\phi}_{C} \leq 1 x_Q\\ \hat{\phi}_{C} & \hat{\phi}_{C} \triangleleft 0 \ , \ \hat{\phi}_{C} \triangleright 1 \end{cases}$

(2)

where

$\boldsymbol{a_{f} = 0 }$

(2)

$b_{f} = \frac{2 y_{Q} - s_{Q}x_{Q}}{x_{Q}}$

(2)

$\boldsymbol{ c_{f} = y_{Q} - s_{Q}x_{Q} }$

(2)

$\boldsymbol{ d_{f} = s_{Q} }$

(2)

$e_{f} = \frac{3 x_{Q} - 2 y_{Q} - s_{Q}x_{Q}}{3 x_{Q} - 2}$

(2)

$f_{f} = \frac{2 y_{Q} + 2 s_{Q} x_{Q} - 2 }{3 x_{Q} - 2}$

(2)

and

$\hat{\phi}_{C}= \hat{\phi}_{C} U^{+}_{f} + \hat{\phi}_{D} U^{-}_{f}$

(1)

HLPA - Hybrid Linear / Parabolic Approximation

Zhu J. Low Diffusive and oscillation-free convection scheme // Communications and Applied Numerical Methods. 1991. 7, N3. 225-232.

Zhu J., Rodi W. A low dispersion and bounded discretization schemes for finite volume computations of incompressible flows // Computational Methods for Applied Mechanics and Engineering. 1991. 92. 87-96

In this scheme, the normalized face value is approximated by a combination of linear and parabolic charachteristics passing through the points, O, Q, and P in the NVD. It satisfies TVD condition and is second-order accurate

Usual variables

$\phi_{f}= \begin{cases} \phi_{f} + \left( \phi_{P} - \phi_{W} \right) \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq 1 \\ \phi_{W} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

Normalized variables - uniform grids

$\hat{\phi_{f}}= \begin{cases} \hat{\phi_{C}} \left( 2 - \hat{\phi_{C}} \right) \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

Normalized variables - non-uniform grids

$\hat{\phi_{f}}= \begin{cases} a_{f} + b_{f} \hat{\phi_{C}} + c_{f} \hat{\phi_{C}}^{2} & 0 \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

where

$\boldsymbol{a_{f} = 0 }$

(2)

$b_{f} = \left(y_{Q}- x^{2}_{Q} \right) / \left(x_{Q}- x^{2}_{Q} \right)$

(2)

$c_{f} = \left(y_{Q}- x_{Q} \right) / \left(x_{Q}- x^{2}_{Q} \right) ,$

(2)

Implementation

Using the switch factors:

for 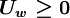$\boldsymbol{U_w \geq 0}$

$\alpha^{+}_{w} = \begin{cases} 1 & \ \mbox{if} \ | \phi_{P} - 2 \phi_{W} + \phi_{WW}| \triangleleft | \phi_{P} - \phi_{WW} | \\ 0 & \mbox{otherwise} \end{cases}$

(2)

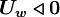
for $\boldsymbol{U_w \triangleleft 0}$

$\alpha^{-}_{w} = \begin{cases} 1 & \ \mbox{if} \ | \phi_{W} - 2 \phi_{P} + \phi_{E}| \triangleleft | \phi_{W} - \phi_{E} | \\ 0 & \mbox{otherwise} \end{cases}$

(2)

and taken all the possible flow directions into account, the un-normalized form of equation can be written as

$\phi_{w} = U^{+}_{w} \phi_{W} + U^{-}_{w} \phi_{P} + \Delta \phi_{w}$

(2)

where

$\Delta \phi_{w} = U^{+}_{w} \alpha^{+}_{w} \left( \phi_{P} - \phi_{W} \right) \frac{\phi_{W} - \phi_{WW}}{\phi_{P} - \phi_{WW}} + U^{-}_{w} \alpha^{-}_{w} \left( \phi_{W} - \phi_{P} \right) \frac{\phi_{P} - \phi_{E}}{\phi_{W} - \phi_{E}}$

(2)

$U^{+}_{w} = 0.5 \left( 1 + \left| U_{w} \right| / U_{w} \right) \ , \ U^{-}_{w} = 1 - U^{+}_{w} \ \ \left( U_{w}\neq 0 \right)$

(2)

LODA - Local Oscillation-Damping Algorithm

J. Zhu and M.A. Leschziner

A local oscillation-damping algorithm for higher-order convection schemes

Comput. Methods Appl. Mech. Engnrng 67 (1988) 355-366

CLAM - Curved-Line Advection Method

Van Leer B. , Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. Journal of Computational Physics 1974; 14:361-370

identical to HLPA

normalised variables - uniform grids

$\hat{\phi_{f}}= \begin{cases} \hat{\phi_{C}} \left( 2 - \hat{\phi_{C}} \right) \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

normalised variables - non-uniform grids (NVSF - compare with HLPA - here is used another variant of notation)

$\hat{\phi}_{f} = \begin{cases} \frac{\hat{\xi}_f - \hat{\xi}^{2}_{C}}{\hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C - \frac{\hat{\xi}_f - \hat{\xi}_{C}}{\hat{\xi}_C \left( 1 - \hat{\xi}_C \right)}\hat{\phi}^{2}_{C} & 0 \leq \hat{\phi}_{C} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

van Leer harmonic

BSOU

G. Papadakis, G. Bergeles.

A locally modified second order upwind scheme for convection terms discretization.

Int. J. Numer. Meth. Heat Fluid Flow, 5.49-62, 1995

MSOU - Monotonic Second Order Upwind Differencing Scheme

Sweby

Koren

bounded CUS

B. Koren

A robust upwind discretisation method for advection, diffusion and source terms

In: Numerical Mthods for Advection-Diffusion Problems, Ed. C.B.Vreugdenhil& B.Koren, Vieweg, Braunscheweigh, p.117, (1993)

H-CUS

bounded CUS

N.P.Waterson H.Deconinck

A unified approach to the design and application of bounded high-order convection schemes

VKI-preprint, 1995-21, (1995)

MLU

B. Noll

Evaluation of a bounded high-resolution scheme for combustor flow computations

AIAA J., vol. 30, No. 1, p.64 (1992)

LPPA - Linear and Piecewise / Parabolic Approximasion

Normalized variables - uniform grids

$\hat{\phi_{f}}= \begin{cases} \frac{9}{4}{\phi}_{C} - \frac{3}{2} {\phi}^{2}_{C} & 0 \leq \hat{\phi}_{C} \leq \frac{1}{2} \\ \frac{1}{4}+\frac{5}{4}{\phi}_{C}-\frac{1}{2}{\phi}^{2}_{C} & \frac{1}{2} \leq \hat{\phi}_{C} \leq 1 \\ \hat{\phi}_{C} & \hat{\phi}_{C} \triangleleft 0 \ , \ \hat{\phi}_{C} \triangleright 1 \end{cases}$

(2)

Normalized variables - non-uniform grids

$\hat{\phi_{f}}= \begin{cases} a_{f}+ b_{f} \hat{\phi}_{C} + c_{f}\hat{\phi}^{2}_{C} & 0 \leq \hat{\phi_{C}} \leq x_{Q} \\ d_{f}+ d_{f} \hat{\phi}_{C} + f_{f}\hat{\phi}^{2}_{C} & x_{Q} \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi}_{C} \triangleleft 0 \ , \ \hat{\phi}_{C} \triangleright 1 \end{cases}$

(2)

where

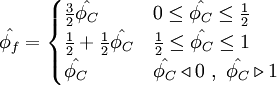
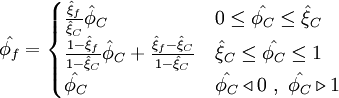
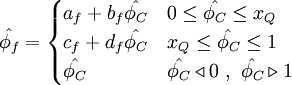
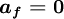
$\boldsymbol{a_{f}= 0}$

(2)

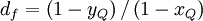
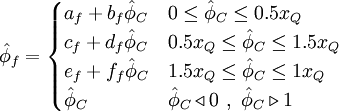
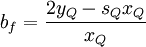
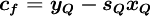
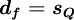
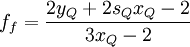
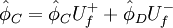
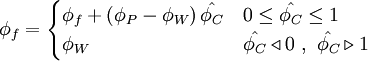
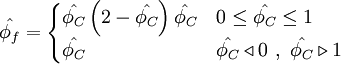
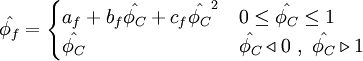
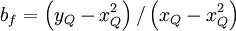
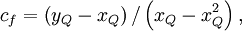
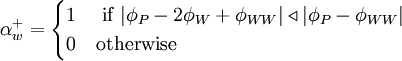
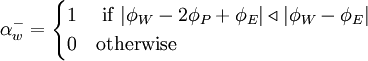
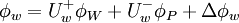
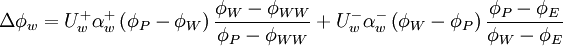
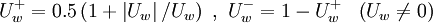
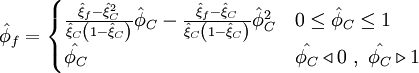
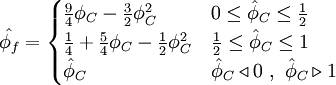
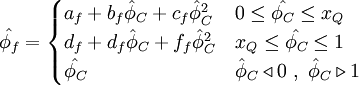
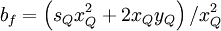
$b_{f}= \left( s_{Q}x^{2}_{Q} + 2x_{Q}y_{Q} \right) / x^{2}_{Q}$

(2)

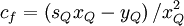
$c_{f}= \left( s_{Q}x_{Q} - y_{Q} \right)/ x^{2}_{Q}$

(2)

$d_{f} = \left[ x^{2}_{Q} + s_{Q} \left( x^{2}_{Q} - x_{Q} \right)+ \left( 1 - 2 x_{Q} \right) \right] / \left( 1 - x_{Q} \right)^{2}$

(2)

$e_{f} = \left[ -2 x_{Q} + s_{Q} \left( 1 - x^{2}_{Q} \right) + 2 x_{Q} y_{Q} \right] / \left( 1 - x_{Q} \right)^{2}$

(2)

$f_{f} = \left[ 1 + s_{Q} \left( x_{Q} - 1 \right) - 2 y_{Q} \right] / \left( 1 - x_{Q} \right)^{2}$

(2)

GAMMA

Jasak H., Weller H.G., Gosman A.D.

High resolution NVD differencing scheme for arbitrarily unstructured meshes

International Journal for Numerical Methods in Fluids

1999, 31: 431-449

$\hat{\phi}_{f}= \begin{cases} \hat{\phi}_C \left[ 1 + \frac{1}{2 \beta_m } \left( 1 - \hat{\phi}_C \right) \right] & 0 \triangleleft \hat{\phi}_C \triangleleft \beta_m \\ \frac{1}{2}\hat{\phi}_{C} + \frac{1}{2} & \beta_m \leq \hat{\phi}_C \leq 1 \\ \hat{\phi}_C & \mbox{elsewhere} \end{cases}$

(2)

$\hat{\phi}_{f}= \begin{cases} \hat{\phi}_C \left[1 + \frac{1}{\beta_m} \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } \left( 1 - \hat{\phi}_C \right) \right] & 0 \triangleleft \hat{\phi}_C \triangleleft \beta_m \\ \frac{ 1 - \hat{\xi}_f }{ 1 - \hat{\xi}_C } \hat{\phi}_C + \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } & \beta_m \leq \hat{\phi}_C \leq 1 \\ \hat{\phi}_C & \mbox{elsewhere} \end{cases}$

(2)

CUBISTA - Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection

M.A. Alves, P.J.Oliveira, F.T. Pinho, A convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection // International Lournal For Numerical Methods in Fluids 2003, 41; 47-75

normalised variables - uniform grid

$\hat{\phi}_{f}= \begin{cases} \frac{7}{4}\hat{\phi}_{C} & 0 \triangleleft \hat{\phi}_C \triangleleft \frac{3}{8} \\ \frac{3}{4}\hat{\phi}_{C} + \frac{3}{8} & \frac{3}{8} \leq \hat{\phi}_C \leq \frac{3}{4} \\ \frac{1}{4}\hat{\phi}_{C} + \frac{3}{4} & \frac{3}{4} \triangleleft \hat{\phi}_C \triangleleft 1 \\ \hat{\phi}_{C} & \mbox{elsewhere} \end{cases}$

(2)

normalised variables - non-uniform grid (NVSF)

$\hat{\phi}_{f}= \begin{cases} \left[1+\frac{\hat{\xi}_f- \hat{\xi}_C}{3\left( 1 - \hat{\xi}_C \right) } \right] \frac{\hat{\xi}_f}{\hat{\xi}_C} \hat{\phi}_C & 0 \triangleleft \hat{\phi}_C \triangleleft \frac{3}{4}\hat{\xi}_C \\ \frac{\hat{\xi}_f \left(1- \hat{\xi}_f \right)}{ \hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C + \frac{\hat{\xi}_f \left( \hat{\xi}_f - \hat{\xi}_C \right)}{1- \hat{\xi}_C} & \frac{3}{4} \hat{\xi}_C \leq \hat{\phi}_C \leq \frac{1 + 2 \left( \hat{\xi}_f - \hat{\xi}_C \right) }{ 2 \hat{\xi}_f - \hat{\xi}_C } \hat{\xi}_C \\ \frac{\hat{\xi}_f \left(1- \hat{\xi}_f \right)}{ \hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C + \frac{\hat{\xi}_f \left( \hat{\xi}_f - \hat{\xi}_C \right)}{1- \hat{\xi}_C} & \frac{1 + 2 \left( \hat{\xi}_f - \hat{\xi}_C \right) }{ 2 \hat{\xi}_f - \hat{\xi}_C } \hat{\xi}_C \triangleleft \hat{\phi}_C \triangleleft 1 \\ \hat{\phi}_C & \mbox{elsewhere} \end{cases}$

(2)

Return to Numerical Methods

Return to Approximation Schemes for convective term - structured grids

Other Schemes (unclassified) - structured grids

From CFD-Wiki

Latest revision as of 21:09, 10 December 2010

Contents

Chakravarthy-Osher limiter

Sweby $\Phi$ - limiter

Superbee limiter

R-k limiter

MINMOD - MINimum MODulus

SOUCUP - Second-Order Upwind Central differnce-first order UPwind

ISNAS - Interpolation Scheme which is Nonoscillatory for Advected Scalars

COPLA - COmbination of Piecewise Linear Approximation

HLPA - Hybrid Linear / Parabolic Approximation

LODA - Local Oscillation-Damping Algorithm

CLAM - Curved-Line Advection Method

van Leer harmonic

BSOU

MSOU - Monotonic Second Order Upwind Differencing Scheme

Koren

H-CUS

MLU

LPPA - Linear and Piecewise / Parabolic Approximasion

GAMMA

CUBISTA - Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection

Views

My wiki

wiki navigation

wiki search

wiki toolbox

@@ Line 16: / Line 16: @@
 J. Comp. Phys., vol. 49, no. 3, pp. 225-232, 1991
+Identical to SOUCUP
+Normalized variables - uniform grids
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi_{f}}=
+\begin{cases}
+\frac{3}{2} \hat{\phi_{C}}               &  0          \leq \hat{\phi_{C}} \leq \frac{1}{2} \\
+\frac{1}{2} + \frac{1}{2} \hat{\phi_{C}} & \frac{1}{2} \leq \hat{\phi_{C}} \leq 1           \\
+\hat{\phi_{C}}                           & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+Normalized variables - non-uniform grids (NVSF)
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi_{f}}=
+\begin{cases}
+\frac{\hat{\xi}_f}{\hat{\xi}_C} \hat{\phi}_C & 0  \leq \hat{\phi_{C}} \leq \hat{\xi}_C \\
+\frac{ 1 - \hat{\xi}_f }{ 1 - \hat{\xi}_C } \hat{\phi}_C + \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } & \hat{\xi}_C  \leq \hat{\phi_{C}} \leq 1 \\
+\hat{\phi_{C}}                           & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
 [[Image:NM_convectionschemes_struct_grids_MINMOD_probe_01.jpg]]
@@ Line 26: / Line 54: @@
-[[Image:NM_convectionschemes_struct_grids_Schemes_SOUCUP_Probe_01.jpg]]
 Normalized variables - uniform grids
@@ Line 97: / Line 124: @@
 Numerical Heat Transfer, Part B, 28:23-38, 1995
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi}_{f}=
+\begin{cases}
+a_{f} + b_{f} \hat{\phi}_{C}  & 0 \leq \hat{\phi}_{C} \leq 0.5 x_Q \\
+c_{f} + d_{f} \hat{\phi}_{C}  & 0.5 x_Q \leq  \hat{\phi}_{C} \leq 1.5 x_Q\\
+e_{f} + f_{f} \hat{\phi}_{C}  & 1.5 x_Q \leq \hat{\phi}_{C} \leq 1 x_Q\\
+\hat{\phi}_{C} & \hat{\phi}_{C} \triangleleft 0 \ , \ \hat{\phi}_{C} \triangleright 1
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+where
+<table width="100%"><tr><td>
+:<math>
+\boldsymbol{a_{f} = 0 }
+</math>
+</td><td width="5%">(2)</td></tr></table>
+<table width="100%"><tr><td>
+:<math>
+b_{f} = \frac{2 y_{Q} - s_{Q}x_{Q}}{x_{Q}}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+<table width="100%"><tr><td>
+:<math>
+\boldsymbol{ c_{f} = y_{Q} - s_{Q}x_{Q}  }
+</math>
+</td><td width="5%">(2)</td></tr></table>
+<table width="100%"><tr><td>
+:<math>
+\boldsymbol{ d_{f} = s_{Q}  }
+</math>
+</td><td width="5%">(2)</td></tr></table>
+<table width="100%"><tr><td>
+:<math>
+e_{f} = \frac{3 x_{Q} - 2 y_{Q} - s_{Q}x_{Q}}{3 x_{Q} - 2}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+<table width="100%"><tr><td>
+:<math>
+f_{f} = \frac{2 y_{Q} + 2 s_{Q} x_{Q} - 2 }{3 x_{Q} - 2}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+and
+<table width="100%"><tr><td>
+<math>
+\hat{\phi}_{C}= \hat{\phi}_{C} U^{+}_{f} + \hat{\phi}_{D} U^{-}_{f}
+</math>
+</td><td width="5%">(1)</td></tr></table>
 == HLPA - Hybrid Linear / Parabolic Approximation ==
@@ Line 177: / Line 263: @@
 \alpha^{+}_{w} =
 \begin{cases}
-& \ if \ | \phi_{P} - 2 \phi_{W} + \phi_{WW}| \triangleleft | \phi_{P} - \phi_{WW} | \\
+& \ \mbox{if} \ | \phi_{P} - 2 \phi_{W} + \phi_{WW}| \triangleleft | \phi_{P} - \phi_{WW} | \\
-& otherwise
+& \mbox{otherwise}
 \end{cases}
 </math>
@@ Line 189: / Line 275: @@
 \alpha^{-}_{w} =
 \begin{cases}
-& \ if \ | \phi_{W} - 2 \phi_{P} + \phi_{E}| \triangleleft | \phi_{W} - \phi_{E} | \\
+& \ \mbox{if} \ | \phi_{W} - 2 \phi_{P} + \phi_{E}| \triangleleft | \phi_{W} - \phi_{E} | \\
-& otherwise
+& \mbox{otherwise}
 \end{cases}
 </math>
@@ Line 218: / Line 304: @@
 [[Image:NM_convectionschemes_struct_grids_Schemes_HLPA_Probe_01.jpg]]
+== LODA - Local Oscillation-Damping Algorithm ==
+J. Zhu and M.A. Leschziner
+A local oscillation-damping algorithm for higher-order convection schemes
+Comput. Methods Appl. Mech. Engnrng 67 (1988) 355-366
 == CLAM - Curved-Line Advection Method ==
@@ Line 223: / Line 317: @@
 '''Van Leer B.''' , Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. Journal of Computational Physics 1974; 14:361-370
+identical to HLPA
+normalised variables - uniform grids
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi_{f}}=
+\begin{cases}
+\hat{\phi_{C}} \left( 2 -  \hat{\phi_{C}} \right) \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq 1 \\
+\hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+normalised variables - non-uniform grids (NVSF - compare with HLPA - here is used another variant of notation)
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi}_{f} =
+\begin{cases}
+\frac{\hat{\xi}_f - \hat{\xi}^{2}_{C}}{\hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C - \frac{\hat{\xi}_f - \hat{\xi}_{C}}{\hat{\xi}_C \left( 1 - \hat{\xi}_C \right)}\hat{\phi}^{2}_{C} & 0 \leq \hat{\phi}_{C} \leq 1 \\
+\hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
 == van Leer harmonic ==
@@ Line 266: / Line 385: @@
 AIAA J., vol. 30, No. 1, p.64 (1992)
-== SHARP - Simple High Accuracy Resolution Program ==
-'''B.P.Leonard''', Simple high-accuracy resolution rogram for convective modelling of discontinuities, International J. Numerical Methods Fluids 8 (1988) 1291-1381
 == LPPA - Linear and Piecewise / Parabolic Approximasion ==
@@ Line 294: / Line 411: @@
 a_{f}+ b_{f} \hat{\phi}_{C} + c_{f}\hat{\phi}^{2}_{C} & 0    \leq \hat{\phi_{C}} \leq x_{Q} \\
 d_{f}+ d_{f} \hat{\phi}_{C} + f_{f}\hat{\phi}^{2}_{C} & x_{Q} \leq \hat{\phi_{C}} \leq 1      \\
-\hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1
+\hat{\phi_{C}} & \hat{\phi}_{C} \triangleleft 0 \ , \ \hat{\phi}_{C} \triangleright 1
 \end{cases}
 </math>
@@ Line 338: / Line 455: @@
 == GAMMA ==
+Jasak H., Weller H.G., Gosman A.D.
+High resolution NVD differencing scheme for arbitrarily unstructured meshes
+International Journal for Numerical Methods in Fluids
+, 31: 431-449
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi}_{f}=
+\begin{cases}
+\hat{\phi}_C \left[ 1 + \frac{1}{2 \beta_m } \left( 1 - \hat{\phi}_C \right) \right] & 0 \triangleleft \hat{\phi}_C \triangleleft \beta_m \\
+\frac{1}{2}\hat{\phi}_{C} + \frac{1}{2} & \beta_m \leq \hat{\phi}_C \leq 1 \\
+\hat{\phi}_C & \mbox{elsewhere}
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi}_{f}=
+\begin{cases}
+\hat{\phi}_C \left[1 + \frac{1}{\beta_m} \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } \left( 1 - \hat{\phi}_C \right) \right] & 0 \triangleleft \hat{\phi}_C \triangleleft \beta_m \\
+\frac{ 1 - \hat{\xi}_f }{ 1 - \hat{\xi}_C } \hat{\phi}_C + \frac{ \hat{\xi}_f - \hat{\xi}_C }{ 1 - \hat{\xi}_C } &  \beta_m \leq \hat{\phi}_C \leq 1 \\
+\hat{\phi}_C & \mbox{elsewhere}
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
 == CUBISTA - Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection ==
 '''M.A. Alves, P.J.Oliveira, F.T. Pinho''', A convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection // International Lournal For Numerical Methods in Fluids 2003, 41; 47-75
+normalised variables - uniform grid
+<table width="100%"><tr><td>
+:<math>
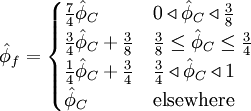
+\hat{\phi}_{f}=
+\begin{cases}
+\frac{7}{4}\hat{\phi}_{C} & 0 \triangleleft \hat{\phi}_C \triangleleft \frac{3}{8} \\
+\frac{3}{4}\hat{\phi}_{C} + \frac{3}{8} & \frac{3}{8} \leq \hat{\phi}_C  \leq \frac{3}{4} \\
+\frac{1}{4}\hat{\phi}_{C} + \frac{3}{4} & \frac{3}{4} \triangleleft \hat{\phi}_C \triangleleft 1 \\
+\hat{\phi}_{C} & \mbox{elsewhere}
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>
+normalised variables - non-uniform grid (NVSF)
+<table width="100%"><tr><td>
+:<math>
+\hat{\phi}_{f}=
+\begin{cases}
+\left[1+\frac{\hat{\xi}_f- \hat{\xi}_C}{3\left( 1 - \hat{\xi}_C \right) } \right] \frac{\hat{\xi}_f}{\hat{\xi}_C} \hat{\phi}_C & 0 \triangleleft \hat{\phi}_C \triangleleft \frac{3}{4}\hat{\xi}_C \\
+\frac{\hat{\xi}_f \left(1- \hat{\xi}_f \right)}{ \hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C + \frac{\hat{\xi}_f \left( \hat{\xi}_f - \hat{\xi}_C \right)}{1- \hat{\xi}_C} & \frac{3}{4} \hat{\xi}_C \leq \hat{\phi}_C \leq \frac{1 + 2 \left( \hat{\xi}_f - \hat{\xi}_C \right) }{ 2 \hat{\xi}_f - \hat{\xi}_C } \hat{\xi}_C \\
+\frac{\hat{\xi}_f \left(1- \hat{\xi}_f \right)}{ \hat{\xi}_C \left( 1 - \hat{\xi}_C \right)} \hat{\phi}_C + \frac{\hat{\xi}_f \left( \hat{\xi}_f - \hat{\xi}_C \right)}{1- \hat{\xi}_C} & \frac{1 + 2 \left( \hat{\xi}_f - \hat{\xi}_C \right) }{ 2 \hat{\xi}_f - \hat{\xi}_C } \hat{\xi}_C  \triangleleft \hat{\phi}_C \triangleleft 1 \\
+\hat{\phi}_C & \mbox{elsewhere}
+\end{cases}
+</math>
+</td><td width="5%">(2)</td></tr></table>

Other Schemes (unclassified) - structured grids

From CFD-Wiki

Latest revision as of 21:09, 10 December 2010

Contents

Chakravarthy-Osher limiter

Sweby - limiter

Superbee limiter

R-k limiter

MINMOD - MINimum MODulus

SOUCUP - Second-Order Upwind Central differnce-first order UPwind

ISNAS - Interpolation Scheme which is Nonoscillatory for Advected Scalars

COPLA - COmbination of Piecewise Linear Approximation

HLPA - Hybrid Linear / Parabolic Approximation

LODA - Local Oscillation-Damping Algorithm

CLAM - Curved-Line Advection Method

van Leer harmonic

BSOU

MSOU - Monotonic Second Order Upwind Differencing Scheme

Koren

H-CUS

MLU

LPPA - Linear and Piecewise / Parabolic Approximasion

GAMMA

CUBISTA - Convergent and Universally Bounded Interpolation Scheme for the Treatment of Advection

Views

My wiki

wiki navigation

wiki search

wiki toolbox

Sweby $\Phi$ - limiter