Streamline
From CFD-Wiki
(Difference between revisions)
m |
|||
| (2 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
A line in the fluid whose tangent is everywhere parallel to the local velocity vector <math>(u,v,w)</math> instantaneously is a streamline. The family of streamlines at time <math>t</math> are solutions of | A line in the fluid whose tangent is everywhere parallel to the local velocity vector <math>(u,v,w)</math> instantaneously is a streamline. The family of streamlines at time <math>t</math> are solutions of | ||
| - | <math> | + | :<math> |
\frac{dx}{u(x,y,z,t)} = \frac{dy}{v(x,y,z,t)} = \frac{dz}{w(x,y,z,t)} | \frac{dx}{u(x,y,z,t)} = \frac{dy}{v(x,y,z,t)} = \frac{dz}{w(x,y,z,t)} | ||
</math> | </math> | ||
| Line 9: | Line 9: | ||
In two dimensions and for [[Axisymmetric flow | axisymmetric flows]], a [[stream function]] exists which is constant on each streamline. | In two dimensions and for [[Axisymmetric flow | axisymmetric flows]], a [[stream function]] exists which is constant on each streamline. | ||
| - | ==Related | + | ==Related pages== |
*[[Path line]] | *[[Path line]] | ||
Latest revision as of 00:22, 23 November 2005
A line in the fluid whose tangent is everywhere parallel to the local velocity vector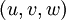 
instantaneously is a streamline. The family of streamlines at time 
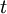are solutions of
Streamlines cannot intersect since the velocity at any point is unique.
In two dimensions and for axisymmetric flows, a stream function exists which is constant on each streamline.
