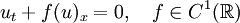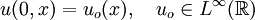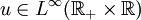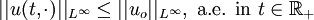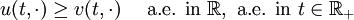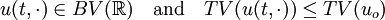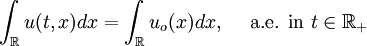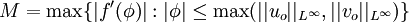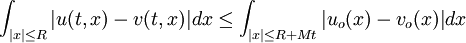Kruzkov theorem
From CFD-Wiki
(Difference between revisions)
| (One intermediate revision not shown) | |||
| Line 46: | Line 46: | ||
</math> | </math> | ||
| - | * '''Finite domain of dependence''': If <math>u, v</math> are two entropy solutions, <math>u_o, v_o \in L^\infty</math> and | + | * '''Finite domain of dependence''': If <math>u, v</math> are two entropy solutions, corresponding to initial conditions <math>u_o, v_o \in L^\infty</math> and |
| Line 60: | Line 60: | ||
u_o(x) - v_o(x) | d x | u_o(x) - v_o(x) | d x | ||
</math> | </math> | ||
| + | |||
| + | ==Related pages== | ||
| + | |||
| + | *[[Monotone scheme]] | ||
| + | *[[TVD scheme]] | ||
| + | *[[Monotonicity preserving scheme]] | ||
Latest revision as of 03:45, 30 September 2005
The scalar Cauchy problem
with initial condition
has a unique entropy solution
which fulfills (important for numerics)
- Stability
- Monotone solution: If
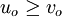 a.e. in
a.e. in 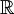 then
then
- TV-diminishing: If
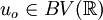 then
then
- Conservation: If
 then
then
- Finite domain of dependence: If
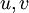 are two entropy solutions, corresponding to initial conditions
are two entropy solutions, corresponding to initial conditions  and
and
then