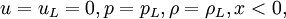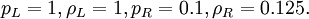CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Shock tube problem

Shock tube problem

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
m (Reverted edits by C4tc4Tsitc (Talk) to last version by Jola)
 
(4 intermediate revisions not shown)
Line 1: Line 1:
-
The test case involves the 1-D Euler equation describing the flow.The initial condition is given by  
+
'''Shock tube problem''' is a special case of [[Riemann problem]] with velocities on both sides of discontinuity set to zero. It is often used as a test case for validation of numerical codes, because analytical solutions are available.The initial condition is given by  
-
:<math> u\equiv u_L ,p=p_L,\rho=\rho_L,x<x_o </math>
+
:<math>u=u_L=0 , p=p_L , \rho=\rho_L, x<0,</math>
-
:<math> u\equiv u_R ,p=p_R,\rho=\rho_R,x>x_o </math>
+
:<math>u=u_R=0 , p=p_R , \rho=\rho_R, x>0.</math>
-
where <math> p_L>p_R </math> diaphragm being located at <math> x=x_o </math>
+
-
Two cases are considered and the flow is simulated using Roe first-order scheme and Steger-Warming  vector splitting scheme.
 
-
:Case 1 <math> p_R \equiv 1.2*10^4 Pa,p_L=10^5 Pa,u_L=u_R=0,\rho_R=0.125,\rho_L=1.0 kg/m^3 ,x_o=5 m ,t_f=0.0061 s </math>
+
A well-known special case is the Sod problem (Sod, 1978) with initial conditions
-
:Case 2 <math> p_R \equiv 1.2*10^3 Pa,p_L=10^5 Pa,u_L=u_R=0,\rho_R=0.01,\rho_L=1.0 kg/m^3 ,x_o=5 m ,t_f=0.0039 s </math>
+
:<math>p_L=1, \rho_L=1, p_R=0.1, \rho_R=0.125.</math>
-
 
+
-
The computational domain is <math> [0,2x_o] </math>.The boundary conditions are set equal to the intial conditions of the undisturbed gas.The computations are carried out with 600 grid points.
+

Latest revision as of 14:18, 19 December 2008

Shock tube problem is a special case of Riemann problem with velocities on both sides of discontinuity set to zero. It is often used as a test case for validation of numerical codes, because analytical solutions are available.The initial condition is given by

u=u_L=0 , p=p_L , \rho=\rho_L, x<0,
u=u_R=0 , p=p_R , \rho=\rho_R, x>0.


A well-known special case is the Sod problem (Sod, 1978) with initial conditions

p_L=1, \rho_L=1, p_R=0.1, \rho_R=0.125.
Retrieved from "https://ns.cfd-online.com/Wiki/Shock_tube_problem"
My wiki