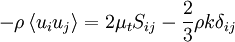Linear eddy viscosity models
From CFD-Wiki
(Difference between revisions)
m |
|||
| (5 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Turbulence modeling}} | {{Turbulence modeling}} | ||
| - | These are turbulence models in which the [[Introduction to turbulence/Reynolds averaged equations|Reynolds stresses]] as obtained from a [[Introduction to turbulence/Reynolds averaged equations|Reynolds averaging of the Navier-Stokes equations]] are modelled by a ''linear constitutive relationship'' with the ''mean'' flow straining field, | + | These are turbulence models in which the [[Introduction to turbulence/Reynolds averaged equations|Reynolds stresses]], as obtained from a [[Introduction to turbulence/Reynolds averaged equations|Reynolds averaging of the Navier-Stokes equations]], are modelled by a ''linear constitutive relationship'' with the ''mean'' flow straining field, as: |
:<math> | :<math> | ||
| - | - \rho \left\langle u_{i} u_{j} \right\rangle = \mu_{t} | + | - \rho \left\langle u_{i} u_{j} \right\rangle = 2 \mu_{t} S_{ij} - \frac{2}{3} \rho k \delta_{ij} |
</math> | </math> | ||
| - | where <math>\mu_{t} </math> is the coefficient termed turbulence "viscosity" (also called the eddy viscosity) | + | where |
| + | |||
| + | :*<math>\mu_{t} </math> is the coefficient termed turbulence "viscosity" (also called the eddy viscosity) | ||
| + | :*<math>k = \frac{1}{2} \left( \left\langle u_{1} u_{1} \right\rangle + \left\langle u_{2} u_{2} \right\rangle + \left\langle u_{3} u_{3} \right\rangle \right)</math> is the mean turbulent kinetic energy | ||
| + | :*<math>S_{ij}= \frac{1}{2} \left[ \frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}} \right] - \frac{1}{3} \frac{\partial U_{k}}{\partial x_{k}} \delta_{ij} | ||
| + | </math> is the ''mean'' strain rate | ||
| + | |||
| + | |||
| + | :Note that that inclusion of <math>\frac{2}{3} \rho k \delta_{ij}</math> in the linear constitutive relation is required by tensorial algebra purposes when solving for [[Two equation models|two-equation turbulence models]] (or any other turbulence model that solves a transport equation for <math>k</math>. | ||
| - | |||
| - | |||
| - | |||
This linear relationship is also known as ''the Boussinesq hypothesis''. For a deep discussion on this linear constitutive relationship, check section [[Introduction to turbulence/Reynolds averaged equations]]. | This linear relationship is also known as ''the Boussinesq hypothesis''. For a deep discussion on this linear constitutive relationship, check section [[Introduction to turbulence/Reynolds averaged equations]]. | ||
| + | |||
| + | There are several subcategories for the linear eddy-viscosity models, depending on the number of (transport) equations solved for to compute the eddy viscosity coefficient. | ||
| + | |||
| + | # [[Algebraic turbulence models|Algebraic models]] | ||
| + | # [[One equation turbulence models|One equation models]] | ||
| + | # [[Two equation models]] | ||
| + | |||
[[Category:Turbulence models]] | [[Category:Turbulence models]] | ||
Latest revision as of 18:38, 7 June 2011
These are turbulence models in which the Reynolds stresses, as obtained from a Reynolds averaging of the Navier-Stokes equations, are modelled by a linear constitutive relationship with the mean flow straining field, as:
where
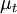 is the coefficient termed turbulence "viscosity" (also called the eddy viscosity)
is the coefficient termed turbulence "viscosity" (also called the eddy viscosity)
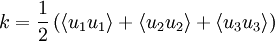 is the mean turbulent kinetic energy
is the mean turbulent kinetic energy
![S_{ij}= \frac{1}{2} \left[ \frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}} \right] - \frac{1}{3} \frac{\partial U_{k}}{\partial x_{k}} \delta_{ij}](/W/images/math/b/c/3/bc3208f532c9a8eeac8e38becd118e0a.png) is the mean strain rate
is the mean strain rate
- Note that that inclusion of
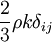 in the linear constitutive relation is required by tensorial algebra purposes when solving for two-equation turbulence models (or any other turbulence model that solves a transport equation for
in the linear constitutive relation is required by tensorial algebra purposes when solving for two-equation turbulence models (or any other turbulence model that solves a transport equation for 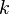 .
.
This linear relationship is also known as the Boussinesq hypothesis. For a deep discussion on this linear constitutive relationship, check section Introduction to turbulence/Reynolds averaged equations.
There are several subcategories for the linear eddy-viscosity models, depending on the number of (transport) equations solved for to compute the eddy viscosity coefficient.

 model
model
 model
model