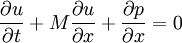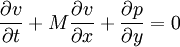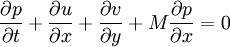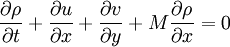2-D linearised Euler equation
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| - | Problem Definition | + | == Problem Definition == |
:<math> \frac{\partial u}{\partial t}+M \frac{\partial u}{\partial x}+\frac{\partial p}{\partial x}=0 </math> | :<math> \frac{\partial u}{\partial t}+M \frac{\partial u}{\partial x}+\frac{\partial p}{\partial x}=0 </math> | ||
:<math> \frac{\partial v}{\partial t}+M \frac{\partial v}{\partial x}+\frac{\partial p}{\partial y}=0 </math> | :<math> \frac{\partial v}{\partial t}+M \frac{\partial v}{\partial x}+\frac{\partial p}{\partial y}=0 </math> | ||
| Line 5: | Line 5: | ||
:<math> \frac{\partial \rho}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial \rho}{\partial x}=0 </math> | :<math> \frac{\partial \rho}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial \rho}{\partial x}=0 </math> | ||
where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow. | where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow. | ||
| - | + | == Domain == [-50,50]*[-50,50] | |
| - | + | == Initial Condition == | |
| - | + | == Boundary Condition == | |
| - | + | == Numerical Method == | |
| - | + | == Results == | |
| - | + | == Reference == | |
| + | *{{reference-paper|author=Williamson, Williamson|year=1980|title=Low Storage Runge-Kutta Schemes|rest=Journal of Computational Physics, Vol.35, pp.48–56}} | ||
| + | |||
| + | *{{reference-paper|author=Lele, Lele, S. K.|year=1992|title=Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics|rest=Journal of Computational Physics, Vol. 103, pp 16–42}} | ||
Revision as of 02:10, 8 October 2005
Contents |
Problem Definition
where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow. == Domain == [-50,50]*[-50,50]
Initial Condition
Boundary Condition
Numerical Method
Results
Reference
- Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.
- Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.