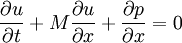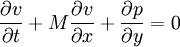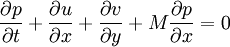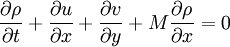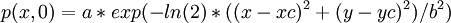2-D linearised Euler equation
From CFD-Wiki
(Difference between revisions)
| Line 15: | Line 15: | ||
4th order low storage RK in time | 4th order low storage RK in time | ||
== Results == | == Results == | ||
| + | Pressure | ||
| + | No mean flow | ||
| + | [[Image:Nomeanflow.jpg]] | ||
| + | Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1) | ||
| + | |||
== Reference == | == Reference == | ||
*{{reference-paper|author=Williamson, Williamson|year=1980|title=Low Storage Runge-Kutta Schemes|rest=Journal of Computational Physics, Vol.35, pp.48–56}} | *{{reference-paper|author=Williamson, Williamson|year=1980|title=Low Storage Runge-Kutta Schemes|rest=Journal of Computational Physics, Vol.35, pp.48–56}} | ||
*{{reference-paper|author=Lele, Lele, S. K.|year=1992|title=Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics|rest=Journal of Computational Physics, Vol. 103, pp 16–42}} | *{{reference-paper|author=Lele, Lele, S. K.|year=1992|title=Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics|rest=Journal of Computational Physics, Vol. 103, pp 16–42}} | ||
Revision as of 07:37, 12 November 2005
Contents |
Problem Definition
where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow.
Domain
[-50,50]*[-50,50]
Initial Condition
Boundary Condition
Characteristic Boundary Condition
Numerical Method
4th Order Compact scheme in space 4th order low storage RK in time
Results
Pressure
No mean flow
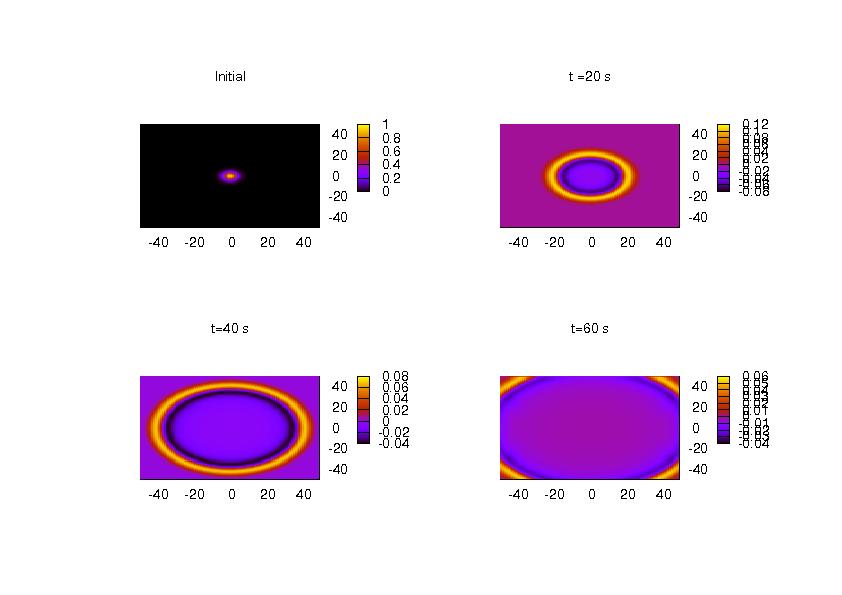 Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1)
Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1)
Reference
- Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.
- Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.