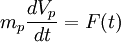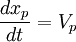Two phase flow

From CFD-Wiki

Revision as of 12:01, 24 September 2007

Introduction

article in progress

Importance of two phase flow in industrial configurations

Two phase flow phenomena occur in various industrial application in all fluid mechanics application fiels. Aerospace, automotive, nuclear applications, etc. In all this domain, prediction of two phase behaviour is important. Prediction of liquid spray in an internal combustion engine should enable us to have a better control on combustion process and then to reduce pollutant emissions. Controlling water - steam equilibrium in a coller system enable to prevent from industrial accident, de-icing/anti-icing of aircraft on the ground etc. Any other examples can be quoted here.

Overview of the different available approach

Two main family can be distinguished to model two phase flow, depending of the two phase configuration approach. In case of dispersed configuration a lagrangian approach is suitable. Such an approach consists in following dropplets (or bubbles) during then movement. This is done by applying external force on the particle and solving acceleration, then velocity and finally position. On the other hand, two phase flow can be solve with an eulerien approach. As in all eulerian framework, this approach consists in considering inlet and outlet flux in a given volume. In such an eulerian approach, two family can be distinguished : Mixture model and Two fluids model, those two approach will be detailed in corresponding section bellow.

Lagrangian dispersed two-phase flow modelling

The main goal in Lagrangien approaches is to statiscally particle history in given flow fields. The starting point in Lagrangien approach is the fundamental law of dynamics:

Where 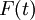stands for the resulting force on the particle. Resolution of these equations requires the knowledge of the instantaneous velocity of the fluid at particle position. The problem is thus to track fluid particles along the discrete particle trajectory. A fluid particle instantaneously owns the velocity of the surrounding fluid and the simulation of its trajectory relies on a quite simple equation such as:

dispersed phase was treated using the lagrangian reference frame; the main goal of this approach is to statistically represent particle history in given flow fields. The trajectories of the particles are computed on the basis of the equation of motion corrected by Odar and Hamilton [12]. This equation was established with the following assumption: -The particles are rigid sphere. -The particles are not rotating. -Particle-particle interactions are neglected. It was demonstrated that the dominant forces are the drag and the gravity. The equation of motion can be written as:

The mathematical expression for the drag coefficient is:

The instantaneous fluid velocity u is decomposed into a mean part which is known (from turbulence model prediction) and a fluctuating part u’. In 2D description, we have to determine a vector of correlated random variables: U’= (ui'(0), uj’ (0)... ui’ (nt), uj’ (nt) ...) where u’(nt) is the fluid fluctuating velocity at time nt. U’ is determinate Starting from a vector Y(yi) of non correlated random numbers with a Gaussian distribution (<yi>=0 and<yiyj>=ij), It is important to keep in mind that particle dispersion is roughly proportional to the turbulence time/length scales.

Mixture model for two phase flow

Basics of the mixture model

MAC approach

VOF method

Eulerian Two fluids approach

Basics of the two fluids approach

Interfacial exchange closures

Turbulence modelling in such a context

Conclusion

References

• Gosman A. D., Ionnides I. E. (1981), "Aspects of computer simulation of liqued fuelled combustors", AIAA aerospace sciences meeting, paper 81-0323, St.louis,MO.
• Fox, R.O. (2003), Computational Models for Turbulent Reacting Flows, ISBN 0-521-65049-6,Cambridge University Press.