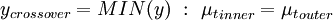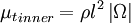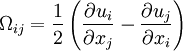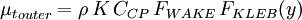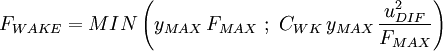From CFD-Wiki
(Difference between revisions)
Revision as of 11:10, 8 September 2005
The Baldwin-Lomax model is a two-layer algebraic model which gives 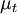 as a function of the local boundary layer velocity profile. The eddy-viscosity,
as a function of the local boundary layer velocity profile. The eddy-viscosity, 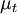 , is given by:
, is given by:
![\mu_t = \left\{
\begin{array}{ll}
{\mu_t}_{inner} & y \leq y_{crossover} \\[1.5ex]
{\mu_t}_{outer} & y > y_{crossover}
\end{array}
\right.](/W/images/math/6/2/a/62aea5700d426d32d39f008c74eb985f.png)
| (1) |
Where 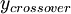 is the smallest distance from the surface where
is the smallest distance from the surface where 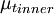 is equal to
is equal to 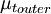 :
:
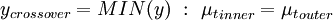
| (2) |
The inner region is given by the Prandtl - Van Driest formula:
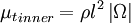
| (3) |
Where
- Failed to parse (unknown function\renewcommand): \renewcommand{\exp}[1]{e^{#1}} l = k y \left( 1 - \exp{\frac{-y^+}{A^+}} \right)
| (4) |

| (5) |
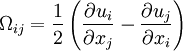
| (6) |
The outer region is given by:
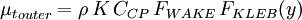
| (7) |
Where
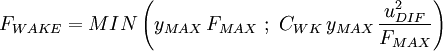
| (7) |
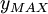 and
and 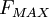 are determined from the maximum of the function:
are determined from the maximum of the function:
| :Failed to parse (unknown function\renewcommand): \renewcommand{\exp}[1]{e^{#1}} F(y) = y \left| \Omega \right| \left(1-\exp{\frac{-y^+}{A^+}} \right)
| (32) |
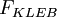 is the intermittency factor given by:
is the intermittency factor given by:
:![F_{KLEB}(y) = \left[1 + 5.5 \left( \frac{y \, C_{KLEB}}{y_{MAX}} \right)^6
\right]^{-1}](/W/images/math/9/b/d/9bde77641b7e232fa3e083d3e59795c4.png) | (32) |
 is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
: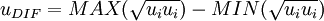 | (32) |
\begin{table}[ht]
\begin{center}
\begin{tabular}{|c|c|c|c|c|c|}
\hline
Failed to parse (syntax error): A^+<math> & <math>C_{CP}<math> & <math>C_{KLEB}<math> & <math>C_{WK}<math> & <math>k<math> & <math>K<math> \\ \hline 26 & 1.6 & 0.3 & 0.25 & 0.4 & 0.0168 \\ \hline \end{tabular} \caption{Model Constants, Baldwin-Lomax Model} \end{center} \end{table} Table 1 gives the model constants present in the formulas above. Note that <math>k<math> is a constant, and not the turbulence energy, as in other sections. It should also be pointed out that when using the Baldwin-Lomax model the turbulence energy, <math>k<math>, present in the governing equations, is set to zero. == References == ''Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows'' by B. S. Baldwin and H. Lomax, AIAA Paper 78-257, 1978
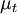 as a function of the local boundary layer velocity profile. The eddy-viscosity,
as a function of the local boundary layer velocity profile. The eddy-viscosity, 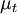 , is given by:
, is given by:
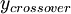 is the smallest distance from the surface where
is the smallest distance from the surface where 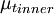 is equal to
is equal to 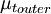 :
:
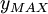 and
and 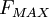 are determined from the maximum of the function:
are determined from the maximum of the function:
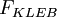 is the intermittency factor given by:
is the intermittency factor given by:
![F_{KLEB}(y) = \left[1 + 5.5 \left( \frac{y \, C_{KLEB}}{y_{MAX}} \right)^6
\right]^{-1}](/W/images/math/9/b/d/9bde77641b7e232fa3e083d3e59795c4.png)
 is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
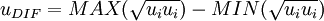

![\mu_t = \left\{
\begin{array}{ll}
{\mu_t}_{inner} & y \leq y_{crossover} \\[1.5ex]
{\mu_t}_{outer} & y > y_{crossover}
\end{array}
\right.](/W/images/math/6/2/a/62aea5700d426d32d39f008c74eb985f.png)