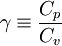Ratio of specific heats
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
| - | The ratio of specific heats (also known as ''adiabatic index''), usually denoted by <math>\gamma</math> is the ratio of specific heat at constant pressure to the specific heat at constant volume | + | The ratio of specific heats (also known as ''adiabatic index''), usually denoted by <math>\gamma</math>, is the ratio of specific heat at constant pressure to the specific heat at constant volume. |
| - | <math> | + | :<math> |
| - | \gamma | + | \gamma \equiv \frac{C_p}{C_v} |
</math> | </math> | ||
| - | The adiabatic index always exceeds unity; for a polytropic gas it is constant. For monatomic gas <math>\gamma=5/3</math>, and for diatomic gases <math>\gamma=7/5</math>, at ordinary temperatures. For air its value is close to that of a diatomic gas, 7/5. | + | The adiabatic index always exceeds unity; for a polytropic gas it is constant. For monatomic gas <math>\gamma=5/3</math>, and for diatomic gases <math>\gamma=7/5</math>, at ordinary temperatures. For air its value is close to that of a diatomic gas, 7/5 = 1.4. |
| + | |||
| + | Sometimes <math>\kappa</math> is used instead of <math>\gamma</math> to denote the specific heat ratio. | ||
Revision as of 10:52, 12 September 2005
The ratio of specific heats (also known as adiabatic index), usually denoted by 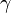 , is the ratio of specific heat at constant pressure to the specific heat at constant volume.
, is the ratio of specific heat at constant pressure to the specific heat at constant volume.
The adiabatic index always exceeds unity; for a polytropic gas it is constant. For monatomic gas 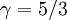 , and for diatomic gases
, and for diatomic gases 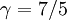 , at ordinary temperatures. For air its value is close to that of a diatomic gas, 7/5 = 1.4.
, at ordinary temperatures. For air its value is close to that of a diatomic gas, 7/5 = 1.4.
Sometimes 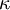 is used instead of
is used instead of 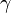 to denote the specific heat ratio.
to denote the specific heat ratio.