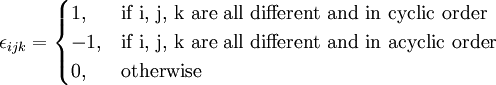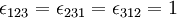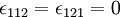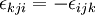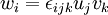Alternating tensor

From CFD-Wiki

Revision as of 04:35, 20 September 2005 (view source) Praveen (Talk | contribs) ← Older edit		Latest revision as of 04:38, 20 September 2005 (view source) Praveen (Talk | contribs)
Line 29:		Line 29:
	:<math>		:<math>
	\epsilon_{kji} = -\epsilon_{ijk}		\epsilon_{kji} = -\epsilon_{ijk}
		+	</math>
		+
		+	This tensor is useful in defining the cross product of two vectors. If <math> w := u \times v</math>, then
		+
		+	:<math>
		+	w_i = \epsilon_{ijk} u_j v_k
	</math>		</math>

---

Latest revision as of 04:38, 20 September 2005

The alternating tensor, also known as Levi-Civita symbol is defined by

Thus

If any index is repeated then the value is zero, e.g.,

If any two indices are interchanged then the sign changes, e.g.,

This tensor is useful in defining the cross product of two vectors. If 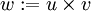, then