Source term linearization
From CFD-Wiki
| Line 21: | Line 21: | ||
<math> S_P = -3T_P^{*2} </math> <br> | <math> S_P = -3T_P^{*2} </math> <br> | ||
| - | =References= | + | ==References== |
#{{reference-book|author=Patankar, S.V.|year=1980|title=Numerical Heat Transfer and Fluid Flow|rest=ISBN 0070487405, Hemisphere Publishing Corporation, USA.}} | #{{reference-book|author=Patankar, S.V.|year=1980|title=Numerical Heat Transfer and Fluid Flow|rest=ISBN 0070487405, Hemisphere Publishing Corporation, USA.}} | ||
#{{reference-paper|author=Murthy, Jayathi Y.|year=1998|title=Numerical Methods in Heat, Mass, and Momentum Transfer|rest=Draft Notes, Purdue University ([http://widget.ecn.purdue.edu/%7Ejmurthy/me608/main.pdf/ download])}} | #{{reference-paper|author=Murthy, Jayathi Y.|year=1998|title=Numerical Methods in Heat, Mass, and Momentum Transfer|rest=Draft Notes, Purdue University ([http://widget.ecn.purdue.edu/%7Ejmurthy/me608/main.pdf/ download])}} | ||
#{{reference-paper|author=[http://webfea-lb.fea.aub.edu.lb/fea/me/CFD/ Darwish, Marwan]|year=2003|title=CFD Course Notes|rest=Notes, American University of Beirut}} | #{{reference-paper|author=[http://webfea-lb.fea.aub.edu.lb/fea/me/CFD/ Darwish, Marwan]|year=2003|title=CFD Course Notes|rest=Notes, American University of Beirut}} | ||
| - | |||
Revision as of 05:55, 7 December 2005
Introduction
In seeking the solution of the general transport equation for a scalar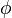 
, the main objective is to correctly handle the non-linearities by transforming them into linear form and then iteratively account for the non-linearity. The source term plays a central role in this respect when it is non-linear. For example, in radiation heat transfer, the source term in energy equation is expressed as fourth powers in the temperature.
When the source is constant and independent of the conserved scalar, the finite volume method assumes that the value of S prevails of the control volume and thus can be easily integrated. For a given control volume P, we obtain
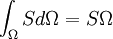
Picard's Method
Picard's method is the most popular method used in conjunction with the finite volume method. For a given control volume P, we start by writing the source term as
where 
denotes the constant part of S and 
denotes the coefficient of 
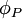(not the value of S at P). This allows us to place 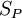in the coefficients for .
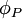Let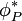 
denote the value of 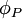at the current itertaion. We now write a Taylor series expansion of S about 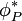as
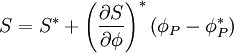
therefore
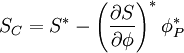
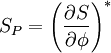
where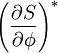 
is the gradient of S evaluated at .
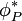As an illustrative example, consider 
. Following Picard's method, we have
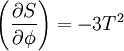
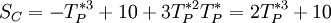
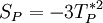
References
- Patankar, S.V. (1980), Numerical Heat Transfer and Fluid Flow, ISBN 0070487405, Hemisphere Publishing Corporation, USA..
- Murthy, Jayathi Y. (1998), "Numerical Methods in Heat, Mass, and Momentum Transfer", Draft Notes, Purdue University (download).
- Darwish, Marwan (2003), "CFD Course Notes", Notes, American University of Beirut.
