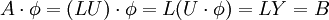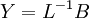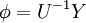LU decomposition
From CFD-Wiki
(Difference between revisions)
(towards a uniform notation for linear systems : A*Phi = B) |
|||
| Line 1: | Line 1: | ||
== LU Solvers == | == LU Solvers == | ||
| - | For the system of equations | + | For the system of equations <math>A\cdot\phi=B</math>. <br> |
The solvers based on factorization are widely popular. The factorization of a non singular matrix '''A''' in two matrices '''L''' and '''U''', called lower and upper matrices, leads to a direct procedure for the evaluation of the inverse of the matrix. Thus making it possible to calculate the solution vector with given source vector. | The solvers based on factorization are widely popular. The factorization of a non singular matrix '''A''' in two matrices '''L''' and '''U''', called lower and upper matrices, leads to a direct procedure for the evaluation of the inverse of the matrix. Thus making it possible to calculate the solution vector with given source vector. | ||
It now remains a two step process: a forward substitution followed by a backward substitution. | It now remains a two step process: a forward substitution followed by a backward substitution. | ||
| Line 7: | Line 7: | ||
: Calculate '''LU''' factors of '''A''' | : Calculate '''LU''' factors of '''A''' | ||
| - | :: | + | ::<math> A\cdot \phi = (LU)\cdot \phi = L(U\cdot\phi)=LY=B</math> |
| - | : Solve | + | : Solve <math>LY=B</math> by <i>forward substitution</i> |
| - | :: | + | :: <math> Y = L^{-1} B</math> |
| - | : Solve | + | : Solve <math>U\phi =Y</math> by <i>backward substitution</i> |
| - | :: | + | :: <math> \phi = U^{-1}Y</math> |
| + | {{stub}} | ||
---- | ---- | ||
Revision as of 20:42, 15 December 2005
LU Solvers
For the system of equations 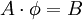 .
.
The solvers based on factorization are widely popular. The factorization of a non singular matrix A in two matrices L and U, called lower and upper matrices, leads to a direct procedure for the evaluation of the inverse of the matrix. Thus making it possible to calculate the solution vector with given source vector.
It now remains a two step process: a forward substitution followed by a backward substitution.
Algorithm
- Calculate LU factors of A
- Solve
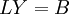 by forward substitution
by forward substitution
-
- Solve
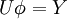 by backward substitution
by backward substitution
-
Return to Numerical Methods