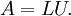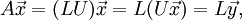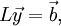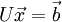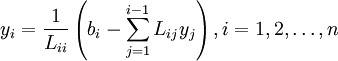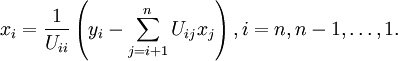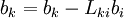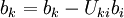CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > LU decomposition

LU decomposition

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
(towards a uniform notation for linear systems : A*Phi = B)
(Added material, used \vec for vectors, still needs more factorization info)
Line 1: Line 1:
-
== LU Solvers ==
+
== Description ==
-
For the system of equations <math>A\cdot\phi=B</math>. <br>
+
Consider the system of equations <math>A\vec{x}=\vec{b}</math>, where <math>A</math> is an <math>n\times n</math> nonsingular matrix.  <math>A</math> may be decomposed into an lower triangular part <math>L</math> and an upper triangular part <math>U</math> that will lead us to a direct procedure for the solution of the original system. This decomposition procedure is quite useful when more than one right-hand side (more than one <math>\vec{b}</math>) is to be used.
-
The solvers based on factorization are widely popular. The factorization of a non singular matrix '''A''' in two matrices '''L''' and '''U''', called lower and upper matrices, leads to a direct procedure for the evaluation of the inverse of the matrix. Thus making it possible to calculate the solution vector with given source vector.
+
-
It now remains a two step process: a forward substitution followed by a backward substitution.  
+
-
== Algorithm ==
+
The algorithm is relatively straightforward - first, we determine the upper and lower triangular parts:
-
:  Calculate '''LU''' factors of '''A'''
+
:<math>A = LU.</math>
-
::<math> A\cdot \phi = (LU)\cdot \phi = L(U\cdot\phi)=LY=B</math>
+
-
:  Solve <math>LY=B</math> by <i>forward substitution</i>
+
-
:: <math> Y = L^{-1} B</math>
+
-
:  Solve <math>U\phi =Y</math> by <i>backward substitution</i>
+
-
:: <math> \phi = U^{-1}Y</math>
+
-
{{stub}}
+
Then,
-
----
+
 
 +
:<math> A \vec{x} = (LU) \vec{x} = L(U\vec{x})=L\vec{y},</math>
 +
 
 +
where <math>y=Ux</math>.  Once we solve the system
 +
 
 +
:<math>L\vec{y} = \vec{b},</math>
 +
 
 +
we will be able to find the solution to the original system by solving
 +
 
 +
:<math>U\vec{x} = \vec{b}</math>
 +
 
 +
The first solution is a foward substitution, while the second solution is a backward substitution.  Both can be done efficiently once the factorization is available.  The forward substitution may be expressed as
 +
 
 +
:<math>
 +
y_i  = {1 \over {L_{ii} }}\left( {b_i  - \sum\limits_{j = 1}^{i-1} {L_{ij} y_j } } \right),
 +
i = 1,2,\ldots,n</math>
 +
 
 +
and the backward substitution process may be expressed as
 +
 
 +
:<math>
 +
x_i  = {1 \over {U_{ii} }}\left( {y_i  - \sum\limits_{j = i + 1}^n {U_{ij} x_j } } \right),
 +
i = n,n-1,\ldots,1.</math>
 +
 
 +
== Algorithm ==
 +
''Add factorization here''<br>
 +
Forward substitution <br>
 +
:    for k:=1 step until n do <br>
 +
::    for i:=1 step until k-1 <br>
 +
:::    <math>b_k=b_k-L_{ki}b_{i}</math> <br>
 +
::    end loop (i) <br>
 +
::    <math>b_{k}=b_{k}/L_{kk}</math><br>
 +
:      end loop (k)
 +
Backward substitution
 +
:    for k:=n stepdown until 1 do <br>
 +
::    for i:=k+1 step until n <br>
 +
:::    <math>b_k=b_k-U_{ki}b_{i}</math> <br>
 +
::    end loop (i) <br>
 +
::    <math>x_{k}=b_{k}/U_{kk}</math><br>
 +
:      end loop (k)
 +
== Important Considerations ==
 +
As with [[Gaussian elimination]],  LU decomposition is probably best used for relatively small, relatively non-sparse systems of equations (with small and non-sparse open to some interpretation).  For larger and/or sparse problems, it would probably be best to either use an iterative method or use a direct solver package (e.g. [http://www.cse.psu.edu/~raghavan/software.html DSCPACK]) as opposed to writing one of your own.
-
----
+
If one has a single lefthand-side matrix and many right-hand side vectors, then LU decomposition would be a good solution procedure to consider.  At the very least, it should be faster than solving each system separately with Gaussian elimination.
-
<i> Return to [[Numerical methods | Numerical Methods]] </i>
+

Revision as of 01:10, 17 December 2005

Description

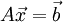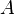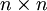Consider the system of equations A\vec{x}=\vec{b}, where A is an n\times n nonsingular matrix. 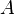A may be decomposed into an lower triangular part 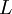L and an upper triangular part 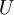U that will lead us to a direct procedure for the solution of the original system. This decomposition procedure is quite useful when more than one right-hand side (more than one \vec{b}) is to be used.

The algorithm is relatively straightforward - first, we determine the upper and lower triangular parts:

A = LU.

Then,

A \vec{x} = (LU) \vec{x} = L(U\vec{x})=L\vec{y},

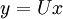where y=Ux. Once we solve the system

L\vec{y} = \vec{b},

we will be able to find the solution to the original system by solving

U\vec{x} = \vec{b}

The first solution is a foward substitution, while the second solution is a backward substitution. Both can be done efficiently once the factorization is available. The forward substitution may be expressed as

y_i = {1 \over {L_{ii} }}\left( {b_i - \sum\limits_{j = 1}^{i-1} {L_{ij} y_j } } \right), i = 1,2,\ldots,n

and the backward substitution process may be expressed as

x_i = {1 \over {U_{ii} }}\left( {y_i - \sum\limits_{j = i + 1}^n {U_{ij} x_j } } \right), i = n,n-1,\ldots,1.

Algorithm

Add factorization here
Forward substitution

for k:=1 step until n do
for i:=1 step until k-1
b_k=b_k-L_{ki}b_{i}
end loop (i)
b_{k}=b_{k}/L_{kk}
end loop (k)

Backward substitution

for k:=n stepdown until 1 do
for i:=k+1 step until n
b_k=b_k-U_{ki}b_{i}
end loop (i)
x_{k}=b_{k}/U_{kk}
end loop (k)

Important Considerations

As with Gaussian elimination, LU decomposition is probably best used for relatively small, relatively non-sparse systems of equations (with small and non-sparse open to some interpretation). For larger and/or sparse problems, it would probably be best to either use an iterative method or use a direct solver package (e.g. DSCPACK) as opposed to writing one of your own.

If one has a single lefthand-side matrix and many right-hand side vectors, then LU decomposition would be a good solution procedure to consider. At the very least, it should be faster than solving each system separately with Gaussian elimination.

Retrieved from "https://ns.cfd-online.com/Wiki/LU_decomposition"
My wiki