Cebeci-Smith model
From CFD-Wiki
(Copied from B-L model, still pretty rough) |
(further clean-up, still needs work) |
||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| - | The Cebeci-Smith [[#References|[ | + | The Cebeci-Smith [[#References|[Smith and Cebeci (1967)]]] is a two-layer algebraic 0-equation model which gives the eddy viscosity, <math>\mu_t</math>, as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the [[Baldwin-Lomax model]], this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the [[Baldwin-Lomax model]], this model requires the determination of of a boundary layer edge. |
== Equations == | == Equations == | ||
| Line 21: | Line 21: | ||
</math></td><td width="5%">(2)</td></tr></table> | </math></td><td width="5%">(2)</td></tr></table> | ||
| - | The inner region is given | + | The inner region is given |
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
:<math> | :<math> | ||
| - | {\mu_t}_{inner} = \rho l^2 \left | + | {\mu_t}_{inner} = \rho l^2 l \left[\left( |
| + | \frac{\partial U}{\partial y}\right)^2 + | ||
| + | \left(\frac{\partial V}{\partial x}\right)^2 | ||
| + | \right]^{1/2}, | ||
</math></td><td width="5%">(3)</td></tr></table> | </math></td><td width="5%">(3)</td></tr></table> | ||
| Line 35: | Line 38: | ||
</math></td><td width="5%">(4)</td></tr></table> | </math></td><td width="5%">(4)</td></tr></table> | ||
| - | + | with the constant <math>\kappa = 0.4</math> and | |
| - | + | ||
| - | \kappa = 0.4 | + | |
| - | </math> | + | |
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
:<math> | :<math> | ||
| - | \left | + | A^+ = 26\left[1+y\frac{dP/dx}{\rho u_\tau^2}\right]^{-1/2}. |
</math></td><td width="5%">(5)</td></tr></table> | </math></td><td width="5%">(5)</td></tr></table> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
The outer region is given by: | The outer region is given by: | ||
| Line 59: | Line 50: | ||
:<math> | :<math> | ||
{\mu_t}_{outer} = \alpha \rho U_e \delta_v^* F_{KLEB}(y;\delta), | {\mu_t}_{outer} = \alpha \rho U_e \delta_v^* F_{KLEB}(y;\delta), | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(6)</td></tr></table> |
where <math>\alpha=0.0168</math>, <math>\delta_v^*</math> is the velocity thickness given by | where <math>\alpha=0.0168</math>, <math>\delta_v^*</math> is the velocity thickness given by | ||
| Line 66: | Line 57: | ||
:<math> | :<math> | ||
\delta_v^* = \int_0^\delta (1-U/U_e)dy, | \delta_v^* = \int_0^\delta (1-U/U_e)dy, | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(7)</td></tr></table> |
and <math>F_{KLEB}</math> is the Klebanoff intermittency function given by | and <math>F_{KLEB}</math> is the Klebanoff intermittency function given by | ||
| Line 74: | Line 65: | ||
F_{KLEB}(y;\delta) = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6 | F_{KLEB}(y;\delta) = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6 | ||
\right]^{-1} | \right]^{-1} | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(8)</td></tr></table> |
| Line 88: | Line 79: | ||
== References == | == References == | ||
| - | * | + | * {{reference-paper|author=Smith, A.M.O. and Cebeci, T. |year=1967|title=Numerical solution of the turbulent boundary layer equations|rest=Douglas aircraft division report DAC 33735}} |
* {{reference-book|author=Wilcox, D.C. |year=1998|title=Turbulence Modeling for CFD|rest=ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc.}} | * {{reference-book|author=Wilcox, D.C. |year=1998|title=Turbulence Modeling for CFD|rest=ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc.}} | ||
Revision as of 15:25, 6 May 2006
Contents |
Introduction
The Cebeci-Smith [Smith and Cebeci (1967)] is a two-layer algebraic 0-equation model which gives the eddy viscosity, 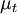 , as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the Baldwin-Lomax model, this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the Baldwin-Lomax model, this model requires the determination of of a boundary layer edge.
, as a function of the local boundary layer velocity profile. The model is suitable for high-speed flows with thin attached boundary-layers, typically present in aerospace applications. Like the Baldwin-Lomax model, this model is not suitable for cases with large separated regions and significant curvature/rotation effects. Unlike the Baldwin-Lomax model, this model requires the determination of of a boundary layer edge.
Equations
|
| (1) |
where 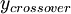 is the smallest distance from the surface where
is the smallest distance from the surface where 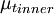 is equal to
is equal to 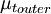 :
:
|
| (2) |
The inner region is given
|
| (3) |
where
|
| (4) |
with the constant 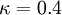 and
and
|
| (5) |
The outer region is given by:
|
| (6) |
where 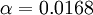 ,
, 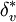 is the velocity thickness given by
is the velocity thickness given by
|
| (7) |
and 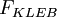 is the Klebanoff intermittency function given by
is the Klebanoff intermittency function given by
|
| (8) |
Model variants
Performance, applicability and limitations
Implementation issues
References
- Smith, A.M.O. and Cebeci, T. (1967), "Numerical solution of the turbulent boundary layer equations", Douglas aircraft division report DAC 33735.
- Wilcox, D.C. (1998), Turbulence Modeling for CFD, ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc..

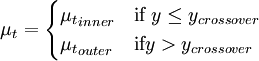
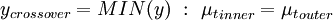
![{\mu_t}_{inner} = \rho l^2 l \left[\left(
\frac{\partial U}{\partial y}\right)^2 +
\left(\frac{\partial V}{\partial x}\right)^2
\right]^{1/2},](/W/images/math/1/2/5/1259b699fd9a5f5544782d6b1f0cc61b.png)
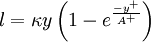
![A^+ = 26\left[1+y\frac{dP/dx}{\rho u_\tau^2}\right]^{-1/2}.](/W/images/math/1/9/8/19839d857afa6c50f418ac133d894115.png)
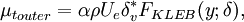
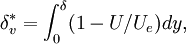
![F_{KLEB}(y;\delta) = \left[1 + 5.5 \left( \frac{y}{\delta} \right)^6
\right]^{-1}](/W/images/math/4/3/3/4331b74159c7e4947a91a3c15e2c8282.png)