Combustion
From CFD-Wiki
(Difference between revisions)
m (→The Wrinkled Regime) |
Combustion (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| - | + | == What is combustion -- physics versus modelling ==Combustion phenomena consist of many physical and chemical processes which exhibit a broad range of time and length scales. A mathematical description of combustion is not always trivial, although some analytical solutions exist for simple situations of laminar flame. Such analytical models are usually restricted to problems in zero or one-dimensional space.= Fundamental Aspects === Main Specificities of Combustion Chemistry ==Combustion can be split into two processes interacting with each other: thermal, and chemical. The chemistry is highly exothermal (this is the reason of its use) but also highly temperature dependent, thus highly self-accelerating. In a simplified form, combustion can be represented by a single irreversible reaction involving 'a' fuel and 'an' oxidizer::<math> \frac{\nu_F}{\bar M_F}Y_F + \frac{\nu_O}{\bar M_O} Y_O \rightarrow Product + Heat </math>Althgough very simplified compared to real chemistry involving hundreds of species (and their individual transport properties) and elemental reactions, this rudimentary chemistry has been the cornerstone of combustion analysis and modelling.The most widely used form for the rate of the above reaction is the Arrhénius law::<math> \dot\omega = \rho A \left ( \frac{Y_F}{\bar M_F} \right )^{n_F} \left (\frac{Y_O}{\bar M_O}\right )^{n_O} \exp^{-T_a/T} </math><math> T_a </math> is the activation temperature, high in combustion, consistently with the temperature dependence.This is where the high non-linearity in temperature is modelled. ''A'' is the pre-exponential constant. One of the interpretation of the Arrhénius law comes from gas kinetic theory: the number of molecules whose kinetic energy is larger than the minimum value allowing a collision to be energetic enough to trig a reaction is proportional to the exponential term introduced above divided by the square root of the temperature. This interpretation allows one to think that the temperature dependence of ''A'' is very weak compared to the exponential term. ''A'' is eventually considered as constant.The reaction rate is also naturally proportional to the molecular density of each of the reactant. Nonetheless, the orders of reaction <math> n_i</math> are different from the stoichiometric coefficients as the single-step reaction is global, not governed by collision for it represents hundreds of elementary reactions.If one goes into the details, combustion chemistry is based on chain reactions, decomposed into three main steps: (i) generation (where radicals are created from the fresh mixture), (ii) branching (where products and new radicals appear from interaction of radicals with reactants), and (iii) termination (where radicals collide and turn into products). The branching step tends to accelerate the production of active radicals (autocatalytic). The impact is nevertheless small compared to the high non-linearity in temperature. This explains why single-step chemistry has been sufficient for most of the combustion modelling work up to now.The fact that a flame is a very thin reaction zone separating, and making the transition between, a frozen mixture and an equilibrium is explained by the high temperature dependence of the reaction term, modelled by a large activation temperature, and a large heat release (the ratio of the burned and fresh gas temperatures is about 7 for typical hydrocarbon flames) leading to a sharp self-acceleration in a very narrow area. To evaluate the order of magnitude of the quantities, the terms in the exponential argument are normalized::<math> \beta=\alpha\frac{T_a}{T_s} \qquad \alpha=\frac{T_s-T_f}{T_s} </math><math>\beta</math> is named the Zeldovitch number and <math>\alpha</math> the heat release factor. Here, <math> T_s</math> has been used instead of <math> T_b</math>, the conventional notation for burned gas temperature (at final equilibrium). <math> T_s</math> is actually <math> T_b</math> for a mixture at stoichiometry and when the flame is adiabatic, i.e. this is the reference highest temperature that can beobtained in the system. That said, typical value for <math>\beta</math> and <math>\alpha</math> are 10 and 0.9, giving a good taste of the level of non-linearity of the combustion process with respect to temperature. Actually, the reaction rate is rewritten as::<math> \dot\omega = \rho A \left ( \frac{Y_F}{\bar M_F} \right )^{n_F} \left (\frac{Y_O}{\bar M_O}\right )^{n_O} \exp^{-\frac{\beta}{\alpha}}\exp^{-\beta\frac{1-\theta}{1-\alpha(1-\theta)}} </math>where the non-dimensionalized temperature is::<math>\theta=\frac{T-T_f}{T_s-T_f}</math>The non-linearity of the reaction rate is seen from the exponential term::* <math> {\mathcal O}(\exp^{-\beta}) </math> for <math>\theta</math> far from unity (in the fresh gas):* <math> {\mathcal O}(1) </math> for <math>\theta</math> close to unity (in the reaction zone close to the burned gas whose temperature must be close to the adiabatic one <math> T_s </math>), more exactly <math> 1-\theta \sim {\mathcal O}(\beta^{-1})</math>[[Image:NonLinearite.jpg|thumb|Temperature Non-Linearity of the Source Term: the Temperature-Dependent Factor of the Reaction Term for Some Values of the Zeldovtich and Heat Release Parameters]]Note that for an infinitely high activation energy, the reaction rate is piloted by a <math>\delta(\theta)</math> function. The figure, beside, illustrates how common values of <math>\beta</math> around 10 tend to make the reaction rate singular around <math>\theta</math> of unity. Two set of values are presented: <math>\beta = 10</math> and <math>\beta = 8</math>. The first magnitude is the representative value while the second one is a smoother one usually used to ease numerical simulations. In the same way, two values for the heat release <math>\alpha</math> 0.9 and 0.75 are explored. The heat release is seen to have a minor impact on the temperature non-linearity.== Transport Equations ==Additionally to the Navier-Stokes equations, at least with variable density, the transport equations for a reacting flow are the energy and species transport equations. In usual notations, the specie ''i'' transport equation is written as::<math>\frac{D \rho Y_i}{D t} = \nabla\cdot \rho D_i\vec\nabla Y_i - \nu_i\bar M_i\dot\omega</math>and the temperature transport equation::<math>\frac{D\rho C_p T}{Dt} = \nabla\cdot \lambda\vec\nabla T + Q\nu_F \bar M_F \dot\omega </math>The diffusion is modelled thanks to Fick's law that is a (usually good) approximation to the rigorous diffusion velocity calculation. Regarding the temperature transport equation, it is derived from the energy transport equation under the assumption of a low-Mach number flow (compressibility and viscous heating neglected). The low-Mach number approximation is suitable for the deflagration regime (as it will be demonstrated [[#Premixed|below]]), which is the main focus of combustion modelling. Hence, the transport equation for temperature, as a simplified version of the energy transport equation, is usually retained for the study of combustion and its modelling.=== Low-Mach Number Equations ===In compressible flows, when the motion of the fluid is not negligible compared to the speed of sound (which is the speed at which the molecules can reorganize themselves), the heap of molecules results in a local increase of pressure and temperature moving as an acoustic wave. It means that, in such a system, a proper reference velocity is the speed of sound and a proper pressure reference is the kinetic pressure. A contrario, in low-Mach number flows, the reference speed is the natural representative speed of the flow and the reference pressure is the thermodynamic pressure. Hence, the set of reference quantities to characterize a low-Mach number flow is given in the table below:Density <math>\rho_o</math> A reference density (upstream, average, etc.)Velocity <math>U_o</math> A reference velocity (inlet average, etc.)Temperature <math>T_o</math> A reference temperature (upstream, average, etc.)Pressure (static) <math>P_o=\rho_o \bar r T_o</math> From Boyle-MariotteLength <math>L_o</math> A reference length (representative of the domain)Time <math>L_o/U_o</math>Energy <math>C_p T_o</math> Internal energy at constant reference pressure The equations for fluid mechanics properly adimensionalized can be written:Mass conservation::<math> \frac{D\rho}{Dt} =0 </math>Momentum::<math>\frac{D\rho\vec U}{Dt}=-\frac{1}{\gamma M}\vec\nabla P+\nabla\cdot\frac{1}{Re}\bar\bar\Sigma</math>Total energy::<math>\frac{D\rho e_T}{Dt}-\frac{1}{RePr}\nabla\cdot\lambda\vec\nabla T=-\frac{\gamma-1}{\gamma}\nabla\cdot P\vec U+\frac{1}{Re}M^2(\gamma-1)\nabla\cdot \vec U\bar\bar\Sigma + \frac{\rho}{C_pT_o(U_o/L_o)}Q\nu_F \bar M_F\dot\omega</math>Specie::<math>\frac{D\rho Y}{Dt}-\frac{1}{ScRe}\nabla\cdot\rho D\vec\nabla Y=-\frac{\rho}{U_o/L_o}\nu\bar M\dot\omega</math>State law::<math> P=\rho T</math>The low-Mach number equations are obtained considering that <math> M^2 </math> is small. 0.1 is usually taken as the limit, which recovers the value of a Mach number of 0.3 to characterize the incompressible regime.Considering the energy equation, in addition to the terms with <math> M^2 </math> in factor in the equation, the total energy reduces to internal energy as: <math> e_T = T/\gamma+M^2(\gamma-1)\vec U^2/2 </math>. Moreover, the work of pressure is considered as negligible because the gradient of pressure is negligible (low-Mach number approximation is indeed also named ''isobaric'' approximation) and the flow is assumed close to a divergence-free state.For the same reason, volumic energy and enthalpy variations are assumed equal as they only differ through the addition of pressure. Hence, redimensionalized, the low-Mach number energy equation leads to the temperature equation as used in combustion analysis::<math>\frac{D\rho C_p T}{Dt} = \nabla\cdot \lambda\vec\nabla T + Q\nu_F \bar M_F \dot\omega </math>______________________________'''Note:''' The species and temperature equations are not closed as the fields of velocity and density also need to be computed. Through intense heat release in a very small area (the jump in temperature in typical hydrocarbon flames is about seven and so is the drop in density in this isobaric process, and the thickness of a flame is of the order of the millimetre), combustion influences the flow field. Nevertheless, the vast majority of combustion modelling has been developed based on the species and temperature equations, assuming simple flow fields.=== The Damköaut;hler Number ===A flame is a reaction zone. From this simple point of view, two aspects have to be considered: (i) the rate at which it is fed by reactants, let call <math> \tau_d </math> the characteristic time, andthe strength of the chemistry to consume them, let call the characteristic chemical time <math> \tau_c </math>. In combustion, the Damköaut;hler number, ''Da'', compares these both time scales and, for that reason, it is one of the most integral non-dimensional groups::<math>Da=\frac{\tau_d}{\tau_c}</math>.If ''Da'' is large, it means that the chemistry has always the time to fully consume the fresh mixture and turn it into equilibrium. Real flames are usually close to this state. The characteristic reaction time, <math> (Ae^{-T_a/T_s})^{-1} </math>, is estimated of the order of the tenth of a ms. When ''Da'' is low, the fresh mixture cannot be converted by a too weak chemistry. The flow remains frozen. This situation happens with ignition or misfire, for instance. The picture of a deflagration lends itself to a description based on the Damköaut;hler number. A reacting wave progresses towards the fresh mixture through preheating of the upstream closest layer. The elevation of the temperature strengthens the chemistry and reduces its characteristic time such that the mixture changes from a low-''Da'' region (far upstream, frozen) to a high-''Da'' region in the flame (intense reaction to equilibrium).== Conservation Laws ==The processus of combustion transforms the chemical enthalpy into sensible enthalpy (i.e. rise the temperature of the gases thanks to the heat released). Simple relations can be drawn between species and temperature by studying the source terms appearing in the above equations::<math> \frac{Y_F}{\nu_F\bar M_F} - \frac{Y_O}{\nu_O\bar M_O} = \frac{Y_{F,u}}{\nu_F\bar M_F} - \frac{Y_{O,u}}{\nu_O\bar M_O} </math>:<math> Y_F + \frac{Cp T}{Q} = Y_{F,u} + \frac{CpT_u}{Q} </math>Hence <math> T_b = T_u + \frac{Q Y_{F,u}}{Cp} </math>, <math> Y_{O,b} = Y_{O,u} - \frac{\nu_O \bar M_O}{\nu_F \bar M_F} Y_{F,u} </math> and <math> Y_{F,b} = 0 </math>. Here, the example has been taken for a lean case.As mentioned in [[#Main Specificities of Combustion Chemistry|Sec. Main Specificities]], the stoichiometric state is used to non-dimensionalize the conservation equations::<math> Y_i^* = Y_{i,u}^* - \theta \qquad ; \qquad Y_i^*=Y_i/Y_{i,s}</math>.A comprehensive form of the reaction rate can be reconstituted to understand the difficulty of numerically resolving the reaction zone::<math> \dot\omega = B \prod_{i=O,F}(Y_{i,u}^*-\theta)^{n_i} \exp{\left ( -\beta\frac{1-\theta}{1-\alpha(1-\theta)}\right)} </math>where <math> B </math> stands for all the constant terms present in this reaction rate, plus density.[[Image:NonLineariteii.jpg|thumb|Source Term versus Temperature]]For the stoichiometric case and a global order of two, the reaction rate is graphed versus the reduced temperature for different values of the heat release and Zeldovitch parameter. A high value of <math>\beta</math> makes the reaction rate very sharp, versus temperature. It means that reaction is significant beyond a temperature level (sometimes called ignition temperature) that is close to one (the exponential term above is non-negligible for <math>1-\theta \sim \beta^{-1}</math>). The heat release has qualitatively the same impact but not so strong. Transposed to the case of a flame sheet, it effectively shows that the reaction exists only in a fraction of the thermal thickness of the flame (the region close to the flame that the latter preheats, hence, where the reduced temperature rises from 0 to 1 here) where the temperature deviates few from the maximal one (density can be assumed as constant and equal to its burned-gas value). Numerically capturing such a sharp reaction zone can be costly and the lower values of <math>\beta</math> and <math>\alpha</math> as presented here are usually preferred whenever possible.Most problems in combustion involve turbulent flows, gas and liquid fuels, and pollution transport issues (products of combustion as well as for example noise pollution). These problems require not only extensive experimental work, but also numerical modelling. All combustion models must be validated against the experiments as each one has its own drawbacks and limits. In this article, we will address the modeling fundamentals only.In addition to the flow parameters used in fluid mechanics,new dimensionless parameters are introduced, the most important of which are the [[Karlovitz number]] and the [[Damkholer number]] which represent ratios of chemical and flow time scales, and the [[Lewis number]] which compares the diffusion speeds of species.The combustion models are often classified on their capability to deal with the different combustion regimes. <br>[[Image:SUMMARY_OF_COMBUSTION_MODELS.jpg]]= Three Combustion Regimes =Depending on how fuel and oxidizer are brought into contact in the combustion system, different combustion modes or regimes are identified. Traditionally, two regimes have been recognized: the ''premixed'' regime and the ''non-premixed'' regime. Over the last two decades, a third regime, sometime considered as a hybrid of the two former ones to a certain extend, has risen. It has been named ''partially-premixed'' regime.== The Non-Premixed Regime ==[[Image:DiffusionFlame.jpg|thumb|Sketch of a diffusion flame]]This regime is certainly the easiest to understand. Everybody has already seen a lighter, candle or gas-powered stove. Basically, the fuel issues from a nozzle or a simple duct into the atmosphere. The combustion reaction is the oxidization of the fuel. Because fuel and oxidizer are in contact only in a limited region but are separated elsewhere (especially in the feeding system) this configuration is the safest. The non-premixed flame has some other advantages. By controlling the flows of both reactants, it is (theoretically) possible to locate the stoichiometric interface, and thus, the location of the flame sheet. Moreover, the strength of the flame can also be controlled through the same process. Depending on the width of the transition region from the oxidizer to the fuel side, the species (fuel and oxidizer) feed the flame at different rates.This is because the diffusion of the species is directly dependent on the unbalance (gradient) of their distribution. A sharp transition from fuel to oxidizer creates intense diffusion of those species towards the flame, increasing its burning rate. This burning rate control through the diffusion process is certainly one of the reasons of the alternate name of such a flame and combustion mode: ''diffusion'' flame and ''diffusion'' regime.Because a diffusion flame is fully determined by the inter-penetration of the fuel and oxidizer streams, it has been convenient to introduce a tracer of the state of the mixture. This is the role of the ''mixture fraction'', usually called ''Z'' or ''f''. Z is usually taken as unity in the fuel stream and is null in the oxidizer stream. It varies linearly between this two bounds such that at any point of a frozen flow the fuel mass fraction is given by <math> Y_F=ZY_{F,o} </math> and the oxidizer mass fraction by <math> Y_O = (1-Z)Y_{O,o} </math>. <math> Y_{F,o} </math> and <math> Y_{O,o} </math> are the fuel and oxidizer mass fractions in the fuel and oxidizer streams, respectively.The mixture fraction posses a transport equation that is expected to not have any source term as a tracer of a mixture must be a conserved scalar. First, the fuel and oxidizer mass fraction transport equations are written in usual notations::<math>\frac{D \rho Y_F}{D t} = \nabla\cdot \rho D\vec\nabla Y_F - \nu_F\bar M_F\dot\omega</math>:<math>\frac{D \rho Y_O}{D t} = \nabla\cdot \rho D\vec\nabla Y_O - \nu_O\bar M_O\dot\omega</math>The two above equations are linearly combined in a single one in a manner that the source term disappears::<math>\frac{D \rho (\nu_O\bar M_O Y_F-\nu_F\bar M_F Y_O)}{D t} = \nabla\cdot \rho D\vec\nabla (\nu_O\bar M_O Y_F-\nu_F\bar M_F Y_O)</math>The quantity <math>(\nu_O\bar M_O Y_F-\nu_F\bar M_F Y_O)</math> is thus a conserved scalar. The last step is to normalize it such that it equals unity in the pure fuel stream (<math> Y_F=Y_{F,o}</math> and <math> Y_O=0 </math>) and is null in the pure oxidizer stream (<math> Y_F=0</math> and <math> Y_O=Y_{O,o} </math>). The resulting normalized passive scalar is the mixture fraction::<math>Z=\frac{\Phi(Y_F/Y_{F,o})-(Y_O/Y_{O,o})+1}{\Phi+1}\qquad \Phi=\frac{\nu_O\bar M_O Y_{F,o}}{\nu_F\bar M_F Y_{O,o}}</math>governed by the transport equation:<math>\frac{D \rho Z}{D t} = \nabla\cdot \rho D\vec\nabla Z </math>The stoichiometric interface location (and thus the approximate location of the flame if the flow is reacting) is where <math>\Phi(Y_F/Y_{F,o})-(Y_O/Y_{O,o}) </math> vanishes (or <math>Y_F</math> and <math> Y_O </math> are both null in the reacting case). This leads to a stoichiometry definition::<math>Z_s=\frac{1}{1+\Phi}</math>As the mixture fraction qualifies the degree of inter-penetration of fuel and oxidizer, the elements originally present in these molecules are conserved and can be directly traced back to the mixture fraction. This has led to an alternate defintion of the mixture fraction, based on ''element conservation''.First, the elemental mass fraction <math> X_{j} </math> of element ''j'' is linked to the species mass fraction <math> Y_i </math>::<math> X_j = \sum_{i=1}^{n} \frac{a_{i,j} \bar M_j}{\bar M_i} Y_i </math>where <math> a_{i,j} </math> is a matrix counting the number of element ''j'' atoms in specie molecule named ''i'' and ''n'' is the number of species in the mixture.The group pictured by the summation above is a linear combination of <math> Y_i </math>. Because the transport equations of species mass fraction, few lines earlier, are also linear, a transport equation for the elemental mass fraction can be written::<math>\frac{D \rho X_j}{D t} = \nabla\cdot \sum_{i=1}^n\frac{a_{i,j}\bar M_j}{\bar M_i}\rho D_i\vec\nabla Y_i</math>For mass is conserved, the linear combination of the source terms vanishes. Furthermore, by taking the same diffusion coefficient <math> D_i </math> for all the species, the elemental mass fraction transport equation has exactly the same form as the specie transport equation (except the source term). Notice that the assumption of equal diffusion coefficient was also made in the previous definition of the mixture fraction and is justified in turbulent combustion modelling by the turbulence diffusivity flattening the diffusion process in high Reynolds number flows. Hence, the elemental mass fraction transport equation has the same structure as the mixture fraction transport equation seen above. Properly renormalized to reach unity in the fuel stream and zero in the oxidizer stream, the elemental mass fraction is a convenient way of determining the mixture fraction field in a flow. Indeed, it is widely used in practice for this purpose.==== Dissipation Rate ====A very important quantity, derived from the mixture fraction concept, is the ''scalar dissipation rate'', usually noted: <math> \chi </math>. In the above introduction to non-premixed combustion, it has been said that a diffusion flame is fully controlled through: (i) the position of the stoichiometric line, dictating where the flame sheet lies; (ii) the gradients of fuel on one side and oxidizer on the other side, dictating the feeding rate of the reaction zone through diffusion and thus the strength of combustion. According the the mixture fraction definition, the location of the stoichiometric line is naturally tracked through the <math>Z_s</math> iso-line and it is seen here how the mixture fraction is a convenient tracer to locate the flame.In the same manner, the mixture fraction field should also be able to give information on the strength of the chemistry as the gradients of reactants are directly linked to the mixture fraction distribution. The feeding rate of the reaction zone is characterized through the inverse of a time. Because it is done through diffusion, it must be obtained through a combination of mixture fraction gradient and diffusion coefficient (dimensional analysis)::<math> \chi_s = \frac{(\rho D)_s}{\rho_s} ||\vec \nabla Z||^2_s \qquad (\rho D)_s = \left ( \frac{\lambda}{C_p} \right )_s</math>where the subscript ''s'' refers to quantities taken effectively where the reacting sheet is supposed to be, close to stoichiometry. This deduction of the scalar dissipation rate, scaling the feeding rate of the flame, is obtained here through physical arguments and is to be derived from equations below in a more mathematical manner. Note that the transport coefficient for the mixture fraction is identified to the one for temperature. This notation is usually used in the literature to emphasize that the rate of temperature diffusion (that is commensurable to the rate of species diffusion) is the retained parameter (as introduced in the following approach highlighting the role of the scalar dissipation rate).Because combustion is highly temperature-dependent, ''T'' is certainly the scalar to which attention must be paid for. The temperature equation in the Low-Mach Number regime ([[#Low-Mach Number Equations|Sec. Low-Mach Number Equations]]) is written below in steady-state::<math>\rho\vec U \cdot \vec\nabla T = \nabla\cdot \frac{\lambda}{C_p}\vec\nabla T + \frac{Q}{C_p}\nu_F \bar M_F \dot\omega </math>In order to make this equation easily tractable, the Howarth-Dorodnitzyn transform and the Chapman approximation are applied.In the Chapman approximation, the thermal dependence of <math>\lambda/C_p</math> is approximated as <math>\rho^{-1}</math>.The Howarth-Dorodnitzyn transform introduces <math>\rho</math> in the space coordinate system: <math> \vec\nabla \rightarrow \rho\vec\nabla \quad ; \quad \nabla\cdot\rightarrow \rho\nabla\cdot</math>. The effect of these both mathematical operations is to `digest' the thermal variation of quantities such as density or transport coefficient. Hence, the temperature equation comes in a simpler mathematical shape::<math>\frac{\rho}{\rho_s}\vec U \cdot \vec\nabla T = \left ( \frac{\lambda}{C_p}\right )_s \nabla\cdot \vec\nabla T + \frac{Q}{\rho\rho_s C_p}\nu_F \bar M_F \dot\omega </math>Here the references are taken in the flame, i.e. close to the stoichiometric line (''s'' subscript).In a non-premixed system, strictly speaking, <math> \vec U </math>, is not really relevant as the flame is fully controlled by the diffusion process. Notwithstanding, in practice, non-premixed flames must be stabilized by creating a strain in the direction of diffusion. This is the reason why the velocity is left in the equation. Because a diffusion flame is fully described by the mixture fraction field, a change in coordinate can be applied::<math> \left (\begin{array}{c}x \\y\end{array}\right ) \longrightarrow \left (\begin{array}{c}x \\Z\end{array}\right )</math>where ''x'' is the coordinate tangential to the iso-<math>Z_s</math> (hence to the flame, in a first approximation) and ''y'' is perpendicular.The Jacobian of the transform is given as::<math> \left [\begin{array}{cc}\frac{\partial x}{\partial x} & \frac{\partial Z}{\partial x} \\\frac{\partial x}{\partial y} & \frac{\partial Z}{\partial y} \end{array}\right ] = \left [\begin{array}{cc}1 & 0 \\0 & l_d^{-1} \end{array}\right ]</math>Note that the diffusive layer of thickness <math>l_d</math> is defined as the region of transition between fuel and oxidizer and is thus given by the gradient of ''Z'' along the ''y'' direction.This transform is applied to the vectorial operators::<math> \nabla\cdot = \nabla_x\cdot+\nabla_y\cdot=\nabla_x\cdot+\nabla_y\cdot Z\nabla_Z\cdot</math>:<math> \vec\nabla = \vec\nabla_x+\vec\nabla_y=\vec\nabla_x+\vec\nabla_y Z\nabla_Z\cdot</math>With this transform, the above temperature equation looks like::<math>\frac{\rho}{\rho_s}\vec U \cdot (\vec\nabla_x T + \vec\nabla Z \nabla_Z\cdot T) = \left (\frac{\lambda}{C_p}\right )_s \left ( \nabla_x\cdot \vec\nabla_x T + \nabla_y\cdot Z \nabla_Z\cdot \vec\nabla_y Z \nabla_Z\cdot T + \nabla_y\cdot Z \nabla_Z\cdot \vec\nabla_x T + \nabla_x\cdot \vec\nabla_y Z \nabla_Z\cdot T \right ) + \frac{Q}{\rho\rho_s C_p}\nu_F \bar M_F \dot\omega </math>As mentioned above, the velocity and the variation along the tangential direction to the main flame structure ''x'' are not supposed to play a major role. By emphasizing the role of the gradient of ''Z'' along ''y'' as a key parameter defining the configuration the following equation is obtained::<math>0 = \left (\frac{\lambda}{C_p}\right )_s ||\vec\nabla_y Z||^2 \Delta_Z T + \frac{Q}{\rho\rho_s C_p}\nu_F \bar M_F \dot\omega </math>This equation (sometimes named the ''flamelet equation'') serves as the basic framework to study the structure of diffusion flames. It highlights the role of the dissipation rate with respect to the strength of the source term and shows that the dissipation rate calibrates the combustion intensity.To describe the structure of the diffusion flame, the ''reduced mixture fraction'' is set::<math> \xi = \frac{Z-Z_s}{Z_s(1-Z_s)\varepsilon} </math>The utility of the reduced mixture fraction is to focus on the reaction zone. This reaction zone is supposed located on the stoichiometric line (this is why the reduced mixture fraction is centred on <math>Z_s</math>) and to be very thin (reason of the introduction of the magnifying factor <math>\varepsilon</math>).== The Premixed Regime ==[[Image:Premixed.jpg|thumb|Sketch of a premixed flame]]In contrast to the non-premixed regime above, the reactants are here well mixed before entering the combustion chamber. Chemical reaction can occur everywhere and this flame can propagate upstream into the feeding system as a subsonic (deflagration regime) chemical wave. This presents lots of safety issues. Some situations prevent them: (i) the mixture is made too rich (lot of fuel compared to oxidizer) or too lean (too much oxidizer) such that the flame is close to its flammability limits (it cannot easily propagate); (ii) the feeding system and regions where the flame is not wanted are designed such that they impose strong heat loss to the flame in order to quench it. For a given thermodynamical state of the mixture (composition, temperature, pressure), the flame has its own dynamics (speed, heat release, etc) on which there is few control: the wave exchanges mass and energy through diffusion process in the fresh gases. On the other hand, those well defined quantities are convenient to describe the flame characteristics. The mechanism of spontaneous propagationtowards fresh gas through the thermal transfer from the combustion zone to the immediate slice of fresh gassuch that the ignition temperature is eventually reached for this latter was highlighted as early as by the end of the 19th century by Mallard and LeChatelier. The reason the chemical wave is contained in a narrow region of reaction propagating upstream is the consequence of the discussion on the non-linearity of the combustion with temperature in the [[#Fundamental Aspects|Sec. Fundamental Aspects]]. It is of interest to compare the orders of magnitude of the temperature dependent term <math> \exp{(-\beta(1-\theta)/(1-\alpha(1-\theta)))}</math> of the reaction source upstream in the fresh gas (<math>\theta\rightarrow 0</math>) and in the reaction zone close to equilibrium temperature (<math>\theta\rightarrow 1 </math>) for the set of representative values: <math> \beta = 10 </math> and <math>\alpha=0.9</math>. It is found that the reaction is about <math>10^{43}</math> times slower in the freshgas than close to the burned gas. It is known that the chemical time scale is about 0.1 ms in the reaction zone of a typical flame, then the typical reaction time in the fresh gas in normal conditions is about <math> 10^{39} s </math>. To be compared with the order of magnitude of the estimated Universe age: <math> 1 0^{17} s </math>. Non-negligible chemistry is only confined in a thin reaction zone stuck to the hot burned gas at equilibrium temperature. In this zone, the [[#Damköaut;hler]] number is high, in contrast to in the fresh mixture. It is natural and convenient to consider that the reaction rate is strictly zero everywhere except in this small reaction zone (one recovers the Dirac-like shape of the reaction profile, provided that one can see the upstream flow as a region of increasing temperature towards the combustion zone and the downstream flow as in fully equilibrium).As the premixed flame is a reaction wave propagating from burned to fresh gases, the basic parameter is known to be the ''progress variable''. In the fresh gas, the progress variable is conventionally put to zero. In the burned gas, it equals unity. Across the flame, the intermediate values describe the progress of the reaction to turn into burned gas the fresh gas penetrating the flame sheet. A progress variable can be set with the help of any quantity like temperature, reactant mass fraction, provided it is bounded by a single value in the burned gas and another one in the fresh gas. The progress variable is usually named ''c'', in usual notations::<math>c=\frac{T-T_f}{T_b-T_f}</math>It is seen that ''c'' is a normalization of a scalar quantity. As mentioned above, the scalar transport equations are assumed linear such that the transport equation for ''c'' can be obtained directly. Actually, the transport equation for ''T'' ([[#Transport Equations|Sec. Transport Equations]]) is linear if constant heat capacity is further assumed (combustion of hydrocarbon in air implies a large excess of nitrogen whose heat capacity is only slightly varying) and the progress variable equation is directly obtained (here for a default of fuel - lean combustion)::<math>\frac{D\rho c}{Dt}=\nabla\cdot\rho D\vec\nabla c + \frac{\nu_F\bar M_F}{Y_{F,u}}\dot\omega \qquad \rho D = \frac{\lambda}{C_p} </math>The fact that the default or excess of fuel has been discussed above leads to the introduction of another quantity: the ''equivalence ratio''. The equivalence ratio, usually noted <math>\Phi</math>, is the ratio of two ratios. The first one is the ratio of the mass of fuel with the mass of oxidizer in the mixture. The second one is the same ratio for a mixture at stoichiometry. Hence, when the equivalence ratio equals unity, the mixture is at stoichiometry. If it is greater than unity, the mixture is named ''rich'' as there is an excess of fuel. In contrast, when it is smaller than unity the mixture is named ''lean''. The equivalence ratio presented here for premixed flames has little connection with the equivalence ratio introduced earlier regarding the non-premixed regime. Basically, the equivalence ratio as defined for non-premixed flames gives the equivalence ratio of a premixed mixture with the same mass of fuel and oxidizer. Moreover, the equivalence ratio as defined for a premixed mixture can be obtained based on the mixture fraction (it is thus the local equivalence ratio at a point in the non-homogeneous mixture described by the mixture fraction). From the definitions given above::<math> \Phi=\frac{Z}{1-Z}\frac{1-Z_s}{Z_s}</math>==== Premixed Flame Péclet Number ====Earlier in this section, it has been said that a premixed flame posses its own dynamics, as a free propagating surface, and has thus characteristic quantities. For this reason, a Péclet number may be defined, based on these quantities. The Péclet number has the same structure as the Reynolds number but the dynamical viscosity is replaced by the ratio of the thermal conductivity and the heat capacity of the mixture. The thickness <math>\delta_L </math> of a premixed flame is essentially thermal. It means that it corresponds to the distance of the temperature rise between fresh and burned gases. This thickness is below the millimetre for conventional flames. The width of the reaction zone inside this flame is even smaller, by about one order of magnitude. This reaction zone is stuck to the hot side of the flame due to the high thermal dependency of the combustion reactions, as seen above. Hence, the flame region is essentially governed by a convection-diffusion process, the source term being negligible in most of it.It is convenient to write the progress variable transport equation in a steady-state framework. The quantities at flame temperature (<math>_f</math>) are used to non-dimensionalize the equation::<math> \overbrace{(\rho S_L)}^{\dot M}\frac{\vec S_L}{S_L}\vec\nabla c = (\rho D)_f \nabla\cdot (\rho D)^* \vec\nabla c</math>Note that the source term is neglected, consistently with what has been said above.This convection-diffusion equation makes appear a first approximation of a flame Péclet number::<math> Pe_f = \frac{\dot M \delta_L}{(\rho D)_f} \approx 1 </math>From the Péclet number, it is possible to obtain an expression for the flame velocity (remembering that <math> \delta_L/S_{L,f} \approx \tau_c</math>, vid. inf. [[#Three Turbulent-Flame Interaction Regimes| Sec. Three Turbulent-Flame Interaction Regimes]])::<math> S_{L,f}^2\approx \frac{(\rho D)_f}{\rho_f \tau_c}</math>For typical hydrocarbon flames, the speed is some tens of centimetres per second and the diffusivity is some<math> 10^{-5} </math> square metres per second. The chemical time in the reaction zone of about one tenth of a millisecond is recovered.==== Details of the Premixed Unstrained Planar Flame ====A plane combustion wave propagating in a homogeneous fresh mixture is the reference case to describe the premixed regime. At constant speed, it is convenient to see the flame at rest with a flowing upstream mixture. This is actually the way propagating flames are usually stabilized. In the frame of description, the physics is 1-D, steady with a uniform (the flame is said unstrained) mass flowing across the system. Two types of equations are thus sufficient to describe the problem, the temperature transport equation and the species transport equations, as in [[#Transport Equations|Sec. Transport Equations]]. The transport coefficients will be chosen as equal: <math> \rho D_i = \lambda / C_p </math> (unity Lewis numbers). Suppose the 1-D domain is described thanks to a conventional (''Ox'') axis with a flame propagating towards negative ''x'' (this is the conventional usage), the boundary conditions are::* in the frozen mixture: :** <math>Y_i \rightarrow Y_{i,u} \qquad ; \qquad x\rightarrow-\infty </math>:** <math>T \rightarrow T_u \qquad ; \qquad x\rightarrow-\infty </math>:* in the burned gas region supposed at equilibrium::** <math>Y_i \rightarrow Y_{i,b} \qquad ; \qquad x\rightarrow+\infty </math>:** <math>T \rightarrow T_b \qquad ; \qquad x\rightarrow+\infty </math>:<math>Y_{i,b}</math> and <math>T_b</math> are obtained from [[#Conservation Laws|Sec. Conservation Laws]].The quantities that have been mentioned just above (scalar and temperature profiles, mass flow rate through the system) are the solution to be sought.According to the discussions above, the temperature transport equation in its full normalized form may be written as (lean /stoichiometric case)::<math> \dot M \frac{\partial \theta}{\partial x} = \frac{\partial \ }{\partial x}\frac{\lambda}{Cp} \frac{\partial \theta}{\partial x} + \frac{\nu_F \bar M_F B}{Y_{F,s}} \prod_{i=O,F}(Y_{i,u}^*-\theta)^{n_i} \exp{-\beta\frac{1-\theta}{1-\alpha(1-\theta)}} </math>This equation is further simplified by the variable change <math>d\xi=\dot M/(\lambda/Cp)dx</math>::<math>\frac{\partial \theta}{\partial \xi}=\frac{\partial^2 \theta}{\partial \xi^2} + \overbrace{\frac{\lambda/Cp}{\dot M^2}\frac{\nu_F \bar M_F B}{Y_{F,s}}}^{\Lambda} \prod_{i=O,F}(Y_{i,u}^*-\theta)^{n_i} \exp{-\beta\frac{1-\theta}{1-\alpha(1-\theta)}}</math>== The Partially-Premixed Regime ==[[Image:ppf.jpg|thumb| Ideal sketch of a partially-premixed flame]]This regime is somewhat less academics and has been recognized two decades ago. It is acknowledged as a hybrid of the premixed and the non-premixed regimes but the degree of interaction of these two modes of combustion to accurately describe a partially-premixed flame is still not well understood. It can be simply pictured by a lifted diffusion flame. Let us consider fuel issuing from a nozzle into the air. If the exit velocity is large enough, for some fuels, the flame lifts off the rim of the nozzle. It means that below the flame base, fuel and oxidizer have room to premix. Hence, the flame base propagates into a premixed mixture. However, it cannot be reduced to a premixed flame (although it is often simplified as this): (i) the mixing is not perfect and the different parts of the flame front constituting the flame base burn in mixtures of different thermodynamical states. This provides those parts with different deflagration capabilities such that the flame base has a complex shape. Indeed, it is convex, naturally leaded by the part burning at stoichiometry, unless `exotic' feeding temperatures are used. (ii) Because the mixture is not homogeneous, transfer of species and temperature driven by diffusion occurs in a direction perpendicular to the propagation of the flame base. Because the flame front is not flat, those transfers act as a connection vehicle across the different parts of the leading front. (iii) The unburned left downstream by the sections of the leading front not burning at stoichiometry diffuse towards each other to form a diffusion flame as described above. The connection of the leading front with the trailing diffusion flame has been evidenced as complicated and the siege of transfers of species and temperature. These two last items are the state-of-the-art difficulties in understanding those flames and do not appear in the models although it has been demonstrated they have a major impact and are certainly a fundamental characteristic of partially-premixed flames.The partially-premixed flame is usually described using ''c'' and ''Z'' as introduced earlier. Because the framework is essentially non-premixed, the mixture fraction is primarily used to describe the flame. Regarding the head of the flame where partial-premixing has an impact, each part of the front is described with a local progress variable. The need of defining a local progress variable is that each section of the partially-premixed front has a different equivalence ratio leading to a different definition of ''c''::<math> c=\frac{T-T_u}{T_b(Z)-T_u}</math>= Three Turbulent-Flame Interaction Regimes =It may appear odd to try to describe here what is the reason of combustion modelling research: the interaction of the turbulence with chemistry. However, one of the first steps in building knowledge in turbulent combustion was the qualitative exploration of what might be the dynamics of a flame in a turbulent environment. This led to what is now known as ''combustion diagrams''. As explained above, the premixed regime lends itself the easiest to such an approach as it exhibits natural intrinsic quantities which are not as objectively identifiable in the other combustion regimes. Note that these quantities may dependon the geometry of the flame: for instance turbulence can bend a flame sheet, leading to a change in its dynamics compared to the flat flame propagating in a medium at rest. In this section, the turbulence-flame interaction modes will be described for a premixed flame. Only remarks will be added regarding the non-premixed and partially-premixed regimes.An integral quantity to assess the interaction between a premixed flame sheet and the turbulenceis the Karlovitz number ''Ka''. It compares the characteristic time of flame displacement with the characteristic time of the smallest structures (that are also the fastest) of the turbulence.:<math> Ka= \frac{\tau_c}{\tau_k}</math><math>\tau_c</math> is the chemical time of the flame. To estimate it, it is necessary to come back to the above progress variable transport equation in a steady-state framework.:<math> \overbrace{(\rho S_L)}^{\dot M}\frac{\vec S_L}{S_L}\vec\nabla c = (\rho D)_f\nabla\cdot (\rho D)^* \vec\nabla c + \dot\omega_c</math>The premixed wave propagates at a speed <math>S_L</math> because it is fed by reactants diffusing inside the combustion zone and which are preheated because temperature diffuses in the reverse direction. The speed at which the flame progresses is thus related to the rate of species diffusion into the reaction zone which are then consumed. As the premixed flame is a free propagating wave whose speed of propagation is only limited by the chemical strength, the characteristic chemical time is based only on the diffusion and the mass flow rate experienced by the flame::<math> \tau_c = \frac{\rho (\rho D)_f}{\dot M^2}</math>The smallest eddies are the ones being dissipated by the viscous forces. Their characteristic time is estimated thanks to a combination of the viscosity and the flux of turbulent energy to be dissipated (also called turbulent dissipation <math> \varepsilon=u'^3/l_t </math>)::<math>\tau_k = \sqrt{\frac{l_t\nu}{u'^3}}</math>Thanks to those definitions of chemical and small structure times, it is possible to give another definition of the Karlovitz number::<math> Ka=\left (\frac{\delta_L}{l_k} \right)^2</math> which is the square of the ratio between the premixed flame thickness and the small structure scale: ''Ka'' actually compares scales. To arrive to this latter result, the three following assumptions must be used: (i) the flame thickness is obtained thanks to the premixed flame Péclet number (''vid. sup.''); (ii) the turbulence small structure (''Kolmogorov eddies'') scale is given by: <math> l_k=(\nu^3/\varepsilon)^{1/4} </math> following the same dimensional argument as for the estimation of its time; and (iii) scalar diffusion scales with viscosity. ==== Remark Regarding the Diffusion Flame ====From what has been presented above, a diffusion flame does not have characteristic scales. Setting a turbulence combustion regime classification for non-premixed flames has still not been answered by research. Some laws of behaviour will only be drawn around the scalar dissipation rate which is the parameter of integral importance for a diffusion flame.Indeed, the dynamics of a diffusion flame is determined by the strain rate imposed by the turbulence. As for the premixed flames, the shortest eddies (Kolmogorov) are the ones having the largest impact. The diffusive layer is thus given by the size of the Kolmogrov eddies: <math> l_d\approx l_k</math> and the typical diffusion time scale (feeding rate of the reaction zone) is given by the characteristic time of the Kolmogorov eddies: <math> \tau_k^{-1}\approx \chi_s</math> as the Reynolds number of the Kolmogorov structures is unity. Here, <math>\chi_s</math> is the sample-averaging of <math>\chi</math> based on (conditioned) stoichiometric conditions, where the flame is expected to be.== The Wrinkled Regime ==[[Image:wrinkled.jpg|thumb| Wrinkled flamelet regime]]This regime is also called the ''flamelet regime''. Basically, it assumes that the flame structure is not affected by turbulence. The flame sheet is convoluted and wrinkled by eddies but none of them is small enough to enter it.Locally magnifying, the laminar flame structure is maintained.This regime exists for a Karlovitz number below unity (vid. sup.), i.e. chemical time smaller than the small structure time or flame thickness smaller than small structure scale. Notwithstanding, the laminar flame dynamics can be disrupted for <math> u'>S_L</math>. In that case, although the flame structure is not altered by the small structures, it can be convected by large structures such that areas of different locations in the front interact. It shows that, even with a small Karlovitz number, the turbulence effect is not always weak.== The Corrugated Regime ==[[Image:Corrugated.jpg|thumb|Corrugated flamelet regime]]The formal definition of a flame is the region of temperature rise. However, the volume where the reaction takes place is about one order of magnitude smaller, embedded inside the temperature rise region and close to its high temperature end. Hence, there exist some levels of turbulence creating eddies able to enter the flame zone but still large enough to not affect the internal reaction sheet. In other words, the flame thermal region is thickened by turbulence but the reaction zone is still in the wrinkled regime.This situation is called the ''Corrugated Regime''.Due to the structure of the Karlovitz number, once written in terms of length scales (vid. sup.), this situation arises for anincrease of the Karlovitz number by two orders of magnitude compared to the value for the wrinkled regime. Hence, in the range <math> 1 < Ka < 100 </math>, the laminar structure of the reaction zone is still preserved but not the one of the preheat zone.== The Thickened Regime ==[[Image:thickened.jpg|thumb|Thickened regime]]In this last case, turbulence is intense enough to generate eddies able to affect the structure of the reaction zone as well. In practice, it is expected that those eddies are in the tail of the energy spectrum such that their lifetime is very short. Their impact on the reaction zone is thus limited.Obviously, ''Ka > 100''. A topological description is of little relevance here and a ''well-stirred reactor model'' fits better.== Reaction mechanisms ==Combustion is mainly a chemical process. Although we can, to some extent, describe a flame without any chemistry information, modelling of the flame propagation requires the knowledge of speeds of reactions, product concentrations, temperature, and other parameters. Therefore fundamental information about reaction kinetics is essential for any combustion model. A fuel-oxidizer mixture will generally combust if the reaction is fast enough to prevail until all of the mixture is burned into products. If the reaction is too slow, the flame will extinguish. If too fast, explosion or even detonation will occur. The reaction rate of a typical combustion reaction is influenced mainly by the concentration of the reactants, temperature, and pressure. A stoichiometric equation for an arbitrary reaction can be written as:<table width="100%"><tr><td>:<math>\sum_{j=1}^{n}\nu' (M_j) = \sum_{j=1}^{n}\nu'' (M_j),</math></td></tr></table>where <math> \nu </math> denotes the stoichiometric coefficient, and <math>M_j</math> stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction. The reaction rate, expressing the rate of disappearance of reactant <b>i</b>, is defined as:<table width="100%"><tr><td>:<math>RR_i = k \, \prod_{j=1}^{n}(M_j)^{\nu'},</math></td></tr></table>in which <b>k</b> is the specific reaction rate constant. Arrhenius found that this constant is a function of temperature only and is defined as:<table width="100%"><tr><td>:<math>k= A T^{\beta} \, exp \left( \frac{-E}{RT}\right)</math></td></table>where <b>A</b> is pre-exponential factor, <b>E</b> is the activation energy, and <math>\beta</math> is a temperature exponent. The constants vary from one reaction to another and can be found in the literature.Reaction mechanisms can be deduced from experiments (for every resolved reaction), they can also be constructed numerically by the '''automatic generation method''' (see [Griffiths (1994)] for a review on reaction mechanisms).For simple hydrocarbons, tens to hundreds of reactions are involved. By analysis and systematic reduction of reaction mechanisms, global reactions (from one to five step reactions) can be found (see [Westbrook (1984)]).== Governing equations for chemically reacting flows ==Together with the usual Navier-Stokes equations for compresible flow (See [[Governing equations]]), additional equations are needed in reacting flows.The transport equation for the mass fraction <math> Y_k </math> of <i>k-th</i> species is:<math>\frac{\partial}{\partial t} \left( \rho Y_k \right) +\frac{\partial}{\partial x_j} \left( \rho u_j Y_k\right) = \frac{\partial}{\partial x_j} \left( \rho D_k \frac{\partial Y_k}{\partial x_j}\right)+ \dot \omega_k</math>where Ficks' law is assumed for scalar diffusion with <math> D_k </math> denoting the species difussion coefficient, and <math> \dot \omega_k </math> denoting the species reaction rate.A non-reactive (passive) scalar (like the mixture fraction <math> Z </math>) is goverened by the following transport equation:<math>\frac{\partial}{\partial t} \left( \rho Z \right) +\frac{\partial}{\partial x_j} \left( \rho u_j Z \right) = \frac{\partial}{\partial x_j} \left( \rho D \frac{\partial Z}{\partial x_j}\right)</math>where <math> D </math> is the diffusion coefficient of the passive scalar.=== RANS equations ===In turbulent flows, [[Favre averaging]] is often used to reduce the scales (see [[Reynolds averaging]]) and themass fraction transport equation is transformed to:<math>\frac{\partial \overline{\rho} \widetilde{Y}_k }{\partial t} +\frac{\partial \overline{\rho} \widetilde{u}_j \widetilde{Y}_k}{\partial x_j}=\frac{\partial} {\partial x_j} \left( \overline{\rho D_k \frac{\partial Y_k} {\partial x_j} } - \overline{\rho} \widetilde{u''_i Y''_k } \right)+ \overline{\dot \omega_k}</math>where the turbulent fluxes <math> \widetilde{u''_i Y''_k} </math> and reaction terms<math> \overline{\dot \omega_k} </math> need to be closed.The passive scalar turbulent transport equation is:<math>\frac{\partial \overline{\rho} \widetilde{Z} }{\partial t} +\frac{\partial \overline{\rho} \widetilde{u}_j \widetilde{Z} }{\partial x_j}=\frac{\partial} {\partial x_j} \left( \overline{\rho D \frac{\partial Z} {\partial x_j} } - \overline{\rho} \widetilde{u''_i Z'' } \right)</math>where <math> \widetilde{u''_i Z''} </math> needs modelling. A common practice is to model the turbulent fluxes using the gradient diffusion hypothesis. For example, in the equation above the flux <math> \widetilde{u''_i Z''} </math> is modelled as:<math>\widetilde{u''_i Z''} = -D_t \frac{\partial \tilde Z}{\partial x_i}</math> where <math> D_t </math> is the turbulent diffusivity. Since <math> D_t >> D </math>, the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.In addition to the mean passive scalar equation,an equation for the Favre variance <math> \widetilde{Z''^2}</math> is often employed:<math>\frac{\partial \overline{\rho} \widetilde{Z''^2} }{\partial t} +\frac{\partial \overline{\rho} \widetilde{u}_j \widetilde{Z''^2} }{\partial x_j}=\frac{\partial}{\partial x_j}\left( \overline{\rho} \widetilde{u''_i Z''^2} \right) - 2 \overline{\rho} \widetilde{u''_i Z'' }- \overline{\rho} \widetilde{\chi}</math>where <math> \widetilde{\chi} </math> is the mean [[Scalar dissipation]] ratedefined as <math> \widetilde{\chi} =2 D \widetilde{\left| \frac{\partial Z''}{\partial x_j} \right|^2 } </math>This term and the variance diffusion fluxes needs to be modelled.=== LES equations ===The [[Large eddy simulation (LES)]] approach for reactive flows introduces equations for the filtered species mass fractions within the compressible flow field.Similar to the [[#RANS equations]], but using Favre filtering insteadof [[Favre averaging]], the filtered mass fraction transport equation is:<math>\frac{\partial \overline{\rho} \widetilde{Y}_k }{\partial t} +\frac{\partial \overline{\rho} \widetilde{u}_j \widetilde{Y}_k}{\partial x_j}=\frac{\partial} {\partial x_j} \left( \overline{\rho D_k \frac{\partial Y_k} {\partial x_j} } -J_j \right)+ \overline{\dot \omega_k}</math>where <math> J_j </math> is the transport of subgrid fluctuations of mass fraction:<math>J_j = \widetilde{u_jY_k} - \widetilde{u}_j \widetilde{Y}_k</math>and has to be modelled.Fluctuations of diffusion coefficients are often ignored and their contributionsare assumed to be much smaller than the apparent turbulent diffusion due to transport of subgrid fluctuations.The first term on the right hand side is then:<math>\frac{\partial} {\partial x_j} \left(\overline{ \rho D_k \frac{\partial Y_k} {\partial x_j} }\right)\approx\frac{\partial} {\partial x_j} \left(\overline{\rho} D_k \frac{\partial \widetilde{Y}_k} {\partial x_j} \right)</math>[[Category:Equations]]== Infinitely fast chemistry ==All combustion models can be divided into two main groups according to the assumptions on the reaction kinetics.We can either assume the reactions to be infinitely fast - compared to e.g. mixing of the species, or comparable to the time scale of the mixing process. The simple approach is to assume infinitely fast chemistry. Historically, mixing of the species is the older approach, and it is still in wide use today. It is therefore simpler to solve for [[#Finite rate chemistry]] models, at the overshoot of introducing errors to the solution.=== Premixed combustion ===Premixed flames occur when the fuel and oxidiser are homogeneously mixed prior to ignition. These flames are not limited only to gas fuels, but also to the pre-vaporised fuels.Typical examples of premixed laminar flames is bunsen burner, where the air enters the fuel stream and the mixture burns in the wake of the riser tube walls forming nice stable flame. Another example of a premixed system is the solid rocket motor where oxidizer and fuel and properly mixed in a gum-like matrix that is uniformly distributed on the periphery of the chamber.Premixed flames have many advantages in terms of control of temperature and products and pollution concentration. However, they introduce some dangers like the autoignition (in the supply system).[[Image:Premixed.jpg]]==== Turbulent flame speed model ======== Eddy Break-Up model ====The Eddy Break-Up model is the typical example of '''mixed-is-burnt''' combustion model. It is based on the work of Magnussen, Hjertager, and Spalding and can be found in all commercial CFD packages. The model assumes that the reactions are completed at the moment of mixing, so that the reaction rate is completely controlled by turbulent mixing. Combustion is then described by a single step global chemical reaction<table width="100%"><tr><td>:<math>F + \nu_s O \rightarrow (1+\nu_s) P</math></td><td width="5%"></td></tr></table>in which <b>F</b> stands for fuel, <b>O</b> for oxidiser, and <b>P</b> for products of the reaction. Alternativelly we can have a multistep scheme, where each reaction has its own mean reaction rate.The mean reaction rate is given by<table width="100%"><tr><td>:<math>\bar{\dot\omega}_F=A_{EB} \frac{\epsilon}{k} min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu},B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right]</math></td><td width="5%"></td></tr></table> where <math>\bar{C}</math> denotes the mean concentrations of fuel, oxidiser, and products respectively. <b>A</b> and <b>B</b> are model constants with typical values of 0.5 and 4.0 respectively. The values of these constants are fitted according to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for <b>all</b> the situations. Care must be taken especially in highly strained regions, where the ratio of <math>k</math> to <math>\epsilon</math> is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.CFD codes usually have some remedies to overcome this problem.This model largely over-predicts temperatures and concentrations of species like <i>CO</i> and other species. However, the Eddy Break-Up model enjoys a popularity for its simplicity, steady convergence, and implementation.==== Bray-Moss-Libby model ======= Non-premixed combustion ===Non premixed combustion is a special class of combustion where fuel and oxidizerenter separately into the combustion chamber. The diffusion and mixing of the two streamsmust bring the reactants together for the reaction to occur.Mixing becomes the key characteristic for diffusion flames.Diffusion burners are easier and safer to operate than premixed burners.However their efficiency is reduced compared to premixed burners.One of the major theoretical tools in non-premixed combustionis the passive scalar [[mixture fraction]] <math> Z </math> which is thebackbone on most of the numerical methods in non-premixed combustion.==== Conserved scalar equilibrium models ====The reactive problem is split into two parts. First, the problem of <i> mixing </i>, which consists of the location of the flame surface which is a non-reactive problem concerning the propagation of a passive scalar; And second, the <i> flame structure </i> problem, which deals with the distribution of the reactive species inside the flamelet.To obtain the distribution inside the flame front we assume it is locally one-dimensional anddepends only on time and the scalar coodinate.We first make use of the following chain rules:<math>\frac{\partial Y_k}{\partial t} = \frac{\partial Z}{\partial t}\frac{\partial Y_k}{\partial Z}</math><br>:<math>\frac{\partial Y_k}{\partial x_j} = \frac{\partial Z}{\partial x_j}\frac{\partial Y_k}{\partial Z}</math> and transformation :<math>\frac{\partial }{\partial t}= \frac{\partial }{\partial t} + \frac{\partial Z}{\partial t} \frac{\partial }{\partial Z}</math>upon substitution into the species transport equation (see [[#Governing Equations for Reacting Flows]]), we obtain:<math>\rho \frac{\partial Y_k}{\partial t} + Y_k \left[\frac{\partial \rho}{\partial t} + \frac{\partial \rho u_j}{\partial x_j}\right]+ \frac{\partial Y_k}{\partial Z} \left[ \rho \frac{\partial Z}{\partial t} + \rho u_j \frac{\partial Z}{\partial x_j} -\frac{\partial}{\partial x_j}\left( \rho D \frac{\partial Z}{\partial x_j} \right)\right]=\rho D \left( \frac{\partial Z}{\partial x_j} \frac{\partial Z}{\partial x_j} \right)\frac{\partial^2 Y_k}{\partial Z^2} + \dot \omega_k</math>The second and third terms in the LHS cancel out due to continuity and mixture fraction transport.At the outset, the equation boils down to:<math>\frac{\partial Y_k}{\partial t} = \frac{\chi}{2} \frac{\partial ^2 Y_k}{\partial Z^2} + \dot \omega_k</math>where <math> \chi = 2 D \left( \frac{\partial Z}{\partial x_j} \right)^2 </math> is called the <b>scalar dissipation</b>which controls the mixing, providing the interaction between the flow and the chemistry.If the flame dependence on time is dropped, even though the field <math> Z </math> still depends on it.:<math> \dot \omega_k= -\frac{\chi}{2} \frac{\partial ^2 Y_k}{\partial Z^2}</math>If the reaction is assumed to be infinetly fast, the resultant flame distribution is in equilibrium.and <math> \dot \omega_k= 0</math>. When the flame is in equilibrium, the flame configuration <math> Y_k(Z) </math> is independent of strain.===== Burke-Schumann flame structure =====The Burke-Schuman solution is valid for irreversible infinitely fast chemistry.With a reaction in the form of<table width="100%"><tr><td>:<math>F + \nu_s O \rightarrow (1+\nu_s) P</math></td><td width="5%"></td></tr></table>If the flame is in equilibrium and therefore the reaction term is 0.Two possible solution exists, one with pure mixing (no reaction)and a linear dependence of the species mass fraction with <math> Z </math>.Fuel mass fraction:<math>Y_F=Y_F^0 Z</math>Oxidizer mass fraction:<math>Y_O=Y_O^0(1-Z)</math>Where <math> Y_F^0 </math> and <math> Y_O^0 </math> are fuel and oxidizer mass fractionsin the pure fuel and oxidizer streams respectively.The other solution is given by a discontinuous slope at stoichiometric mixture fraction<math> Z_{st}</math> and two linear profiles (in the rich and lean side) at eitherside of the stoichiometric mixture fraction.Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.:<math>Y_F=Y_F^0 \frac{Z-Z_{st}}{1-Z_{st}}</math>and oxidizer mass fraction:<math>Y_O=Y_O^0 \frac{Z-Z_{st}}{Z_{st}}</math>== Finite rate chemistry ===== Premixed combustion ======= Coherent flame model ======== Flamelets based on G-equation ======== Flame surface density model ======= Non-premixed combustion ======= Flamelets based on conserved scalar ====Peters (2000) define Flamelets as "thin diffusion layers embedded in a turbulent non-reactive flow field".If the chemistry is fast enough, the chemistry is active within a thin regionwhere the chemistry conditions are in (or close to) stoichiometric conditions, the "flame" surface.This thin region is assumed to be smaller than Kolmogorov length scale and therefore theregion is locally laminar. The flame surface is defined as an iso-surface of a certain scalar <math> Z </math>,mixture fraction in [[#Non premixed combustion]].The same equation used in [[#Conserved scalar models]] for equilibrium chemistryis used here but with chemical source term different from 0:<math> \frac{\partial Y_k}{\partial t} =\frac{\chi}{2} \frac{\partial ^2 Y_k}{\partial Z^2} + \dot \omega_k.</math>This approach is called the Stationary Laminar Flamelet Model (SLFM) and has the advantage thatflamelet profiles <math> Y_k=f(Z,\chi)</math>can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory [[COSILAB]] [http://www.softpredict.com], which can be used for a variety of relevant geometries; see various [http://www.softpredict.com/?page=989 publications that are available for download]. Other software tools are available such as CHEMKIN [http://www.reactiondesign.com] andCANTERA [http://www.cantera.org].===== Flamelets in turbulent combustion =====In turbulent flames the interest is <math> \widetilde{Y}_k </math>.In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scaleand obviously is much smaller than the grid size.It is therefore needed a distribution of the passive scalar within the cell.<math> \widetilde{Y}_k </math> cannot be obtained directly from the flamelets library<math> \widetilde{Y}_k \neq Y_F(Z,\chi) </math>, where <math> Y_F(Z,\chi) </math> correspondsto the value obtained from the flamelets libraries.A generic solution can be expressed as:<math>\widetilde{Y}_k= \int Y_F( \widetilde{Z},\widetilde{\chi}) P(Z,\chi) dZ d\chi</math>where <math> P(Z,\chi) </math> is the joint [[Probability density function | Probability Density Function]] (PDF) of the mixture fractionand scalar dissipation which account for the scalar distribution inside the cell and "a priori"depends on time and space.The most simple assumption is to use a constant distribution of the scalar dissipation within the cell andthe above equation reduces to:<math>\widetilde{Y}_k= \int Y_F(\widetilde{Z},\widetilde{\chi}) P(Z) dZ</math><math> P(Z) </math> is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a [[beta PDF]])can be build depending only on two moments of the scalarmean and variance,<math> \widetilde{Z},Z''</math>.If the mixture fraction and scalar dissipation are consider independent variables,<math> P(Z,\chi) </math>can be written as <math> P(Z) P(\chi)</math>. The PDF of the scalar dissipation is assumed to be log-normal withvariance unity.:<math>\widetilde{Y}_k= \int Y_F(\widetilde{Z},\widetilde{\chi}) P(Z) P(\chi) dZ d\chi</math>In [[Large eddy simulation (LES)]] context (see [[#LES equations]] for reacting flow),the [[probability density function]] is replaced by a [[subgrid PDF]] <math> \widetilde{P}</math>.The same equation hold by replacing averaged values with filtered values.:<math>\widetilde{Y}_k= \int Y_F(\widetilde{Z},\widetilde{\chi}) \widetilde{P}(Z) \widetilde{P}(\chi) dZ d\chi</math>The assumptions made regarding the shapes of the PDFs are still justified. In LES combustion the[[subgrid variance]] is smaller than RANS counterpart (part of the large-scale fluctuations are solved)and therefore the modelled PDFs are thinner.====== Unsteady flamelets ==========Intrinsic Low Dimensional Manifolds (ILDM)====Detailed mechanisms describing ignition, flame propagation and pollutant formation typically involve several hundred species and elementary reactions, prohibiting their use in practical three-dimensional engine simulations. Conventionally reduced mechanisms often fail to predict minor radicals and pollutant precursors. The ILDM-method is an automatic reduction of a detailed mechanism, which assumes local equilibrium with respect to the fastest time scales identified by a local eigenvector analysis. In the reactive flow calculation, the species compositions are constrained to these manifolds. Conservation equations are solved for only a small number of reaction progress variables, thereby retaining the accuracy of detailed chemical mechanisms. This gives an effective way of coupling the details of complex chemistry with the time variations due to turbulence.The intrinsic low-dimensional manifold (ILDM) method {Maas:1992,Maas:1993} is a method for ''in-situ'' reduction of a detailed chemical mechanism based on a local time scale analysis. This method is based on the fact that different trajectories in state space start from a high-dimensional point and quickly relax to lower-dimensional manifolds due to the fast reactions. The movement along these lower-dimensional manifolds, however, is governed by the slow reactions. It exploits the variety of time scales to systematically reduce the detailed mechanism. For a detailed chemical mechanism with N species, N different time scales govern the process. An assumption that all the time scales are relaxed results in assuming complete equilibrium, where the only variables required to describe the system are the mixture fraction, the temperature and the pressure. This results in a zero-dimensional manifold. An assumption that all but the slowest 'n' time scales are relaxed results in a 'n' dimensional manifold, which requires the additional specification of 'n' parameters (called progress variables). In the ILDM method, the fast chemical reactions do not need to be identified a priori. An eigenvalue analysis of the detailed chemical mechanism is carried out which identifies the fast processes in dynamic equilibrium with the slow processes. The computation of ILDM points can be expensive, and hence an in-situ tabulation procedure is used, which enables the calculation of only those points that are needed during the CFD calculation.--[[User:Fredgauss|Fredgauss]] 07:37, 25 August 2006 (MDT)U. Maas, S.B. Pope. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Comb. Flame 88,239, 1992.Ulrich Maas. Automatische Reduktion von Reaktionsmechanismen zur Simulation reaktiver Str¨omungen. Habilitationsschrift, Universit¨at Stuttgart, 1993.==== Conditional Moment Closure (CMC)====In Conditional Moment Closure (CMC) methods we assume that the species mass fractions are all correlated withthe mixture fraction (in non premixed combustion).From [[Probability density function]] we have:<math>\overline{Y_k}= \int <Y_k|\eta> P(\eta) d\eta</math>where <math> \eta </math> is the sample space for <math> Z </math>.CMC consists of providing a set of transport equations for the conditional moments which define theflame structure.Experimentally, it has been observed that temperature and chemical radicals arestrong non-linear functions of mixture fraction. For a given species mass fraction we can decomposedit into a mean and a fluctuation::<math>Y_k= \overline{Y_k} + Y'_k</math>The fluctuations <math> Y_k' </math> are usually very strong in time and space which makes the closureof <math> \overline{\omega_k} </math> very difficult.However, the alternative decomposition:<math>Y_k= <Y_k|\eta> + y'_k</math>where <math> y'_k </math> is the fluctuation around the conditional mean or the "conditional fluctuation".Experimentally, it is observed that <math> y'_k<< Y'_k </math>, which forms the basic assumption of the CMC method.Closures. Due to this property better closure methods can be used reducing the non-linearity of the mass fraction equations.The [[Derivation of the CMC equations]] produces the following CMC transport equationwhere <math> Q \equiv <Y_k|\eta> </math> for simplicity.:<math>\frac{ \partial Q}{\partial t} + <u_j|\eta> \frac{\partial Q}{\partial x_j} =\frac{<\chi|\eta> }{2} \frac{\partial ^2 Q}{\partial \eta^2} + \frac{ < \dot \omega_k|\eta> }{ <\rho| \eta >}</math>In this equation, high order terms in Reynolds number have been neglected.(See [[Derivation of the CMC equations]] for the complete series of terms).It is well known that closure of the unconditional source term<math> \overline {\dot \omega_k} </math> as a function of themean temperature and species (<math> \overline{Y}, \overline{T}</math>) will give rise to large errors.However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.The first order closure<math> < \dot \omega_k|\eta> \approx \dot \omega_k \left( Q, <T|\eta> \right)</math>is a good approximation in zones which are not close to extinction.===== Second order closure =====A second order closure can be obtained if conditional fluctuations are taken into account.For a chemical source term in the form <math> \dot \omega_k = k Y_A Y_B </math> with the rate constant in Arrhenius form<math> k=A_0 T^\beta exp [-Ta/T] </math>the second order closure is (Klimenko and Bilger 1999):<math>< \dot \omega_k|\eta> \approx < \dot \omega_k|\eta >^{FO}\left[1+ \frac{< Y''_A Y''_B |\eta>}{Q_A Q_B}+ \left( \beta + T_a/Q_T \right)\left(\frac{< Y''_A T'' |\eta>}{Q_AQ_T} + \frac{< Y''_B T'' |\eta>}{Q_BQ_T}\right) + ... \right]</math>where <math> < \dot \omega_k|\eta >^{FO} </math> is the first order CMC closure and<math> Q_T \equiv <T|\eta> </math>.When the temperature exponent <math> \beta </math> or <math> T_a/Q_T </math>are large the error of taking the first order approximation increases.Improvement of small pollutant predictions can be obtained using the above reaction rate for selected species like CO and NO.===== Double conditioning =====Close to extinction and reignition. The conditional fluctuations can be very largeand the primary closure of CMC of "small" fluctuations is not longer valid.A second variable <math> h </math> can be chosen to define a double conditioned mass fraction:<math>Q(x,t;\eta,\psi) \equiv <Y_i(x,t) |Z=\eta,h=\psi ></math>Due to the strong dependence on chemical reactions to temperature, <math> h </math>is advised to be a temperature related variable (Kronenburg 2004).Scalar dissipation is not a good choice, due to its log-normal behaviour(smaller scales give highest dissipation). A must better choice is the sensible enthalpyor a progress variable.Double conditional variables have much smaller conditional fluctuations and allowthe existence of points with the same chemical composition which can be fully burning(high temperature) or just mixing (low temperature). The range of applicability is greatly increased and allows non-premixed and premixed problemsto be treated without ad-hoc distinctions.The main problem is the closure of the new terms involving cross scalar transport.The double conditional CMC equation is obtained in a similar manner than the conventionalCMC equations===== LES modelling =====In a LES context a [[conditional filtering]] operator can be definedand <math> Q </math> therefore represents a conditionally filtered reactive scalar.=== Linear Eddy Model ===The Linear Eddy Model (LEM) was first developed by Kerstein(1988).It is an one-dimensional model for representing the flame structure in turbulent flows.In every computational cell a molecular, diffusion and chemical model is defined as:<math>\frac{\partial}{\partial t} \left( \rho Y_k \right) =\frac{\partial}{\partial \eta} \left( \rho D_k \frac{\partial Y_k}{\partial \eta }\right)+ \dot \omega_k</math>where <math> \eta </math>is a spatial coordinate. The scalar distribution obtained can be seen as aone-dimensional reference field between Kolmogorov scale and grid scales.In a second stage a series of re-arranging stochastic event take place.These events represent the effectsof a certain turbulent structure of size <math> l </math>, smaller than the grid size at a location <math> \eta_0 </math>within the one-dimensional domain. This vortex distort the <math> \eta </math> field obtain by the one-dimensional equation,creating new maxima and minima in the interval <math> (\eta_0, \eta + \eta_0) </math>.The vortex size <math> l </math> is chosen randomly based on the inertial scale range while<math> \eta_0 </math> is obtained from a uniform distribution in <math> \eta </math>.The number of events is chosen to match the turbulent diffusivity of the flow.=== PDF transport models ===[[Probability Density Function]] (PDF) methods are not exclusive to combustion, although they are particularly attractive to them. They provided more information than moment closures and they are used to compute inhomegenous turbulent flows, see reviews in Dopazo (1993) and Pope (1994).PDF methods are based on the transport equation of the joint-PDF of the scalars.Denoting <math> P \equiv P(\underline{\psi}; x, t) </math> where<math> \underline{\psi} = ( \psi_1,\psi_2 ... \psi_N) </math> is the phase space for the reactive scalars<math> \underline{Y} = ( Y_1,Y_2 ... Y_N) </math>.The transport equation of the joint PDF is::<math>\frac{\partial <\rho | \underline{Y}=\underline{\psi}> P }{\partial t} + \frac{ \partial <\rho u_j | \underline{Y}=\underline{\psi}> P }{\partial x_j} =\sum^N_\alpha \frac{\partial}{\partial \psi_\alpha}\left[ \rho \dot{\omega}_\alpha P \right]- \sum^N_\alpha \sum^N_\beta \frac{\partial^2}{\partial \psi_\alpha \psi_\beta}\left[ <D \frac{\partial Y_\alpha}{\partial x_i} \frac{\partial Y_\beta}{\partial x_i} | \underline{Y}=\underline{\psi}> \right] P</math>where the chemical source term is closed. Another term appeared on the right hand side which accounts for the effects ofthe molecular mixing on the PDF, is the so called "micro-mixing " term.Equal diffusivities are used for simplicity <math> D_k = D </math>A more general approach is the velocity-composition joint-PDFwith <math> P \equiv P(\underline{V},\underline{\psi}; x, t) </math>, where <math> \underline{V} </math> is the sample space of the velocity field <math> u,v,w </math>. This approach has the advantage of avoiding gradient-diffusionmodelling. A similar equation to the above is obtained combining the momentum and scalar transport equation.The PDF transport equation can be solved in two ways: through a Lagrangian approachusing stochastic methods or in a Eulerian ways using stochastic fields.==== Lagrangian ====The main idea of Lagrangian methods is that the flow can be represented by an ensemble of fluid particles. Central to this approach is the stochastic differential equations and in particular the [[Langevin equation]].==== Eulerian ====Instead of stochastic particles, smooth stochastic fields can be usedto represent the [[probability density function ]] (PDF) of a scalar (or joint PDF) involved in transport (convection), diffusionand chemical reaction (Valino 1998). A similar formulation was proposed by Sabelnikov and Soulard 2005, which removespart of the a-priori assumption of "smoothness" of the stochastic fields.This approach is purely Eulerian and offers implementations advantages compared toLagrangian or semi-Eulerian methods. Transport equations for scalars are often easy to programme and normalCFD algorithms can be used (see [[Discretisation of convective term]]).Although discretization errors are introduced by solving transport equations, this is partially compesated by the error introduced in Lagrangian approaches due to the numerical evaluation of means.A new set of <math> N_s </math> scalar variables(the stochastic field <math> \xi </math>) is used to represent thePDF:<math>P (\underline{\psi}; x,t) = \frac{1}{N} \sum^{N_s}_{j=1} \prod^{N}_{k=1} \delta \left[\psi_k -\xi_k^j(x,t) \right]</math>===Other combustion models======= MMC ====The Multiple Mapping Conditioning (MMC) (Klimenko and Pope 2003) is anextension of the [[#Conditional Moment Closure (CMC)]] approach combined with[[probability density function]] methods. MMClooks for the minimum set of variables that describes the particular turbulent combustionsystem.==== Fractals ====Derived from the [[#Eddy Dissipation Concept (EDC)]].== References ==*{{reference-paper|author=Dopazo, C.|year=1993|title=Recent development in PDF methods|rest=Turbulent Reacting Flows, ed. P. A. Libby and F. A. Williams }}*{{reference-book|author=Fox, R.O.|year=2003|title=Computational Models for Turbulent Reacting Flows|rest=ISBN 0-521-65049-6,Cambridge University Press}}*{{reference-paper|author=Kerstein, A. R.|year=1988|title=A linear eddy model of turbulent scalar transport and mixing|rest=Comb. Science and Technology, Vol. 60,pp. 391}}*{{reference-paper|author=Klimenko, A. Y., Bilger, R. W.|year=1999|title=Conditional moment closure for turbulent combustion|rest=Progress in Energy and Combustion Science, Vol. 25,pp. 595-687}}*{{reference-paper|author=Klimenko, A. Y., Pope, S. B.|year=2003|title=The modeling of turbulent reactive flows based on multiple mapping conditioning|rest=Physics of Fluids, Vol. 15, Num. 7, pp. 1907-1925}}*{{reference-paper|author=Kronenburg, A.,|year=2004|title=Double conditioning of reactive scalar transport equations in turbulent non-premixed flames|rest=Physics of Fluids, Vol. 16, Num. 7, pp. 2640-2648}}*{{reference-paper|author=Griffiths, J. F.|year=1994|title=Reduced Kinetic Models and Their Application to Practical Combustion Systems |rest=Prog. in Energy and Combustion Science,Vol. 21, pp. 25-107}}*{{reference-book|author=Peters, N.|year=2000|title=Turbulent Combustion|rest=ISBN 0-521-66082-3,Cambridge University Press}}*{{reference-book|author=Poinsot, T.,Veynante, D.|year=2001|title=Theoretical and Numerical Combustion|rest=ISBN 1-930217-05-6, R. T Edwards}}*{{reference-paper|author=Pope, S. B.|year=1994|title=Lagrangian PDF methods for turbulent flows|rest=Annu. Rev. Fluid Mech, Vol. 26, pp. 23-63}}*{{reference-paper|author=Sabel'nikov, V.,Soulard, O.|year=2005|title=Rapidly decorrelating velocity-field model as a tool for solving one-point Fokker-Planck equations for probability density functions of turbulent reactive scalars|rest=Physical Review E, Vol. 72,pp. 016301-1-22}}*{{reference-paper|author=Valino, L.,|year=1998|title=A field montecarlo formulation for calculating the probability density function of a single scalar in a turbulent flow|rest=Flow. Turb and Combustion, Vol. 60,pp. 157-172}}*{{reference-paper|author=Westbrook, Ch. K., Dryer,F. L.,|year=1984|title=Chemical Kinetic Modeling of Hydrocarbon Combustion|rest=Prog. in Energy and Combustion Science,Vol. 10, pp. 1-57}}== External links and sources == | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||

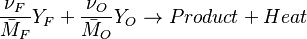 Althgough very simplified compared to real chemistry involving hundreds of species (and their individual transport properties) and elemental reactions, this rudimentary chemistry has been the cornerstone of combustion analysis and modelling.The most widely used form for the rate of the above reaction is the Arrhénius law::
Althgough very simplified compared to real chemistry involving hundreds of species (and their individual transport properties) and elemental reactions, this rudimentary chemistry has been the cornerstone of combustion analysis and modelling.The most widely used form for the rate of the above reaction is the Arrhénius law::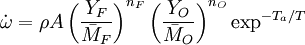
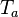 is the activation temperature, high in combustion, consistently with the temperature dependence.This is where the high non-linearity in temperature is modelled. A is the pre-exponential constant. One of the interpretation of the Arrhénius law comes from gas kinetic theory: the number of molecules whose kinetic energy is larger than the minimum value allowing a collision to be energetic enough to trig a reaction is proportional to the exponential term introduced above divided by the square root of the temperature. This interpretation allows one to think that the temperature dependence of A is very weak compared to the exponential term. A is eventually considered as constant.The reaction rate is also naturally proportional to the molecular density of each of the reactant. Nonetheless, the orders of reaction
is the activation temperature, high in combustion, consistently with the temperature dependence.This is where the high non-linearity in temperature is modelled. A is the pre-exponential constant. One of the interpretation of the Arrhénius law comes from gas kinetic theory: the number of molecules whose kinetic energy is larger than the minimum value allowing a collision to be energetic enough to trig a reaction is proportional to the exponential term introduced above divided by the square root of the temperature. This interpretation allows one to think that the temperature dependence of A is very weak compared to the exponential term. A is eventually considered as constant.The reaction rate is also naturally proportional to the molecular density of each of the reactant. Nonetheless, the orders of reaction 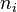 are different from the stoichiometric coefficients as the single-step reaction is global, not governed by collision for it represents hundreds of elementary reactions.If one goes into the details, combustion chemistry is based on chain reactions, decomposed into three main steps: (i) generation (where radicals are created from the fresh mixture), (ii) branching (where products and new radicals appear from interaction of radicals with reactants), and (iii) termination (where radicals collide and turn into products). The branching step tends to accelerate the production of active radicals (autocatalytic). The impact is nevertheless small compared to the high non-linearity in temperature. This explains why single-step chemistry has been sufficient for most of the combustion modelling work up to now.The fact that a flame is a very thin reaction zone separating, and making the transition between, a frozen mixture and an equilibrium is explained by the high temperature dependence of the reaction term, modelled by a large activation temperature, and a large heat release (the ratio of the burned and fresh gas temperatures is about 7 for typical hydrocarbon flames) leading to a sharp self-acceleration in a very narrow area. To evaluate the order of magnitude of the quantities, the terms in the exponential argument are normalized::
are different from the stoichiometric coefficients as the single-step reaction is global, not governed by collision for it represents hundreds of elementary reactions.If one goes into the details, combustion chemistry is based on chain reactions, decomposed into three main steps: (i) generation (where radicals are created from the fresh mixture), (ii) branching (where products and new radicals appear from interaction of radicals with reactants), and (iii) termination (where radicals collide and turn into products). The branching step tends to accelerate the production of active radicals (autocatalytic). The impact is nevertheless small compared to the high non-linearity in temperature. This explains why single-step chemistry has been sufficient for most of the combustion modelling work up to now.The fact that a flame is a very thin reaction zone separating, and making the transition between, a frozen mixture and an equilibrium is explained by the high temperature dependence of the reaction term, modelled by a large activation temperature, and a large heat release (the ratio of the burned and fresh gas temperatures is about 7 for typical hydrocarbon flames) leading to a sharp self-acceleration in a very narrow area. To evaluate the order of magnitude of the quantities, the terms in the exponential argument are normalized::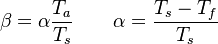
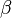 is named the Zeldovitch number and
is named the Zeldovitch number and 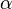 the heat release factor. Here,
the heat release factor. Here, 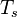 has been used instead of
has been used instead of 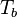 , the conventional notation for burned gas temperature (at final equilibrium).
, the conventional notation for burned gas temperature (at final equilibrium). 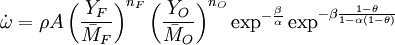 where the non-dimensionalized temperature is::
where the non-dimensionalized temperature is::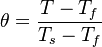 The non-linearity of the reaction rate is seen from the exponential term::*
The non-linearity of the reaction rate is seen from the exponential term::*  for
for 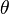 far from unity (in the fresh gas):*
far from unity (in the fresh gas):* 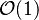 for
for 
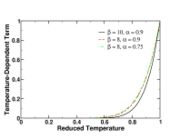
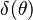 function. The figure, beside, illustrates how common values of
function. The figure, beside, illustrates how common values of 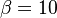 and
and  . The first magnitude is the representative value while the second one is a smoother one usually used to ease numerical simulations. In the same way, two values for the heat release
. The first magnitude is the representative value while the second one is a smoother one usually used to ease numerical simulations. In the same way, two values for the heat release 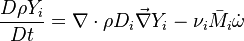 and the temperature transport equation::
and the temperature transport equation::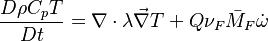 The diffusion is modelled thanks to Fick's law that is a (usually good) approximation to the rigorous diffusion velocity calculation. Regarding the temperature transport equation, it is derived from the energy transport equation under the assumption of a low-Mach number flow (compressibility and viscous heating neglected). The low-Mach number approximation is suitable for the deflagration regime (as it will be demonstrated
The diffusion is modelled thanks to Fick's law that is a (usually good) approximation to the rigorous diffusion velocity calculation. Regarding the temperature transport equation, it is derived from the energy transport equation under the assumption of a low-Mach number flow (compressibility and viscous heating neglected). The low-Mach number approximation is suitable for the deflagration regime (as it will be demonstrated 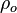 A reference density (upstream, average, etc.)Velocity
A reference density (upstream, average, etc.)Velocity 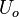 A reference velocity (inlet average, etc.)Temperature
A reference velocity (inlet average, etc.)Temperature 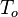 A reference temperature (upstream, average, etc.)Pressure (static)
A reference temperature (upstream, average, etc.)Pressure (static) 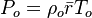 From Boyle-MariotteLength
From Boyle-MariotteLength 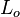 A reference length (representative of the domain)Time
A reference length (representative of the domain)Time 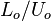 Energy
Energy 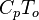 Internal energy at constant reference pressure The equations for fluid mechanics properly adimensionalized can be written:Mass conservation::
Internal energy at constant reference pressure The equations for fluid mechanics properly adimensionalized can be written:Mass conservation::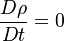 Momentum::
Momentum::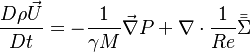 Total energy::
Total energy::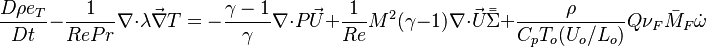 Specie::
Specie::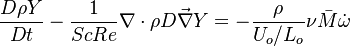 State law::
State law::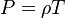 The low-Mach number equations are obtained considering that
The low-Mach number equations are obtained considering that 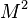 is small. 0.1 is usually taken as the limit, which recovers the value of a Mach number of 0.3 to characterize the incompressible regime.Considering the energy equation, in addition to the terms with
is small. 0.1 is usually taken as the limit, which recovers the value of a Mach number of 0.3 to characterize the incompressible regime.Considering the energy equation, in addition to the terms with  . Moreover, the work of pressure is considered as negligible because the gradient of pressure is negligible (low-Mach number approximation is indeed also named isobaric approximation) and the flow is assumed close to a divergence-free state.For the same reason, volumic energy and enthalpy variations are assumed equal as they only differ through the addition of pressure. Hence, redimensionalized, the low-Mach number energy equation leads to the temperature equation as used in combustion analysis::
. Moreover, the work of pressure is considered as negligible because the gradient of pressure is negligible (low-Mach number approximation is indeed also named isobaric approximation) and the flow is assumed close to a divergence-free state.For the same reason, volumic energy and enthalpy variations are assumed equal as they only differ through the addition of pressure. Hence, redimensionalized, the low-Mach number energy equation leads to the temperature equation as used in combustion analysis::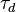 the characteristic time, andthe strength of the chemistry to consume them, let call the characteristic chemical time
the characteristic time, andthe strength of the chemistry to consume them, let call the characteristic chemical time 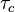 . In combustion, the Damköaut;hler number, Da, compares these both time scales and, for that reason, it is one of the most integral non-dimensional groups::
. In combustion, the Damköaut;hler number, Da, compares these both time scales and, for that reason, it is one of the most integral non-dimensional groups:: .If Da is large, it means that the chemistry has always the time to fully consume the fresh mixture and turn it into equilibrium. Real flames are usually close to this state. The characteristic reaction time,
.If Da is large, it means that the chemistry has always the time to fully consume the fresh mixture and turn it into equilibrium. Real flames are usually close to this state. The characteristic reaction time,  , is estimated of the order of the tenth of a ms. When Da is low, the fresh mixture cannot be converted by a too weak chemistry. The flow remains frozen. This situation happens with ignition or misfire, for instance. The picture of a deflagration lends itself to a description based on the Damköaut;hler number. A reacting wave progresses towards the fresh mixture through preheating of the upstream closest layer. The elevation of the temperature strengthens the chemistry and reduces its characteristic time such that the mixture changes from a low-Da region (far upstream, frozen) to a high-Da region in the flame (intense reaction to equilibrium).== Conservation Laws ==The processus of combustion transforms the chemical enthalpy into sensible enthalpy (i.e. rise the temperature of the gases thanks to the heat released). Simple relations can be drawn between species and temperature by studying the source terms appearing in the above equations::
, is estimated of the order of the tenth of a ms. When Da is low, the fresh mixture cannot be converted by a too weak chemistry. The flow remains frozen. This situation happens with ignition or misfire, for instance. The picture of a deflagration lends itself to a description based on the Damköaut;hler number. A reacting wave progresses towards the fresh mixture through preheating of the upstream closest layer. The elevation of the temperature strengthens the chemistry and reduces its characteristic time such that the mixture changes from a low-Da region (far upstream, frozen) to a high-Da region in the flame (intense reaction to equilibrium).== Conservation Laws ==The processus of combustion transforms the chemical enthalpy into sensible enthalpy (i.e. rise the temperature of the gases thanks to the heat released). Simple relations can be drawn between species and temperature by studying the source terms appearing in the above equations:: :
: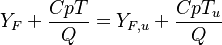 Hence
Hence 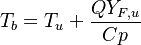 ,
, 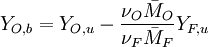 and
and 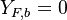 . Here, the example has been taken for a lean case.As mentioned in
. Here, the example has been taken for a lean case.As mentioned in  .A comprehensive form of the reaction rate can be reconstituted to understand the difficulty of numerically resolving the reaction zone::
.A comprehensive form of the reaction rate can be reconstituted to understand the difficulty of numerically resolving the reaction zone::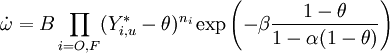 where
where 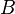 stands for all the constant terms present in this reaction rate, plus density.
stands for all the constant terms present in this reaction rate, plus density.
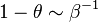 ). The heat release has qualitatively the same impact but not so strong. Transposed to the case of a flame sheet, it effectively shows that the reaction exists only in a fraction of the thermal thickness of the flame (the region close to the flame that the latter preheats, hence, where the reduced temperature rises from 0 to 1 here) where the temperature deviates few from the maximal one (density can be assumed as constant and equal to its burned-gas value). Numerically capturing such a sharp reaction zone can be costly and the lower values of
). The heat release has qualitatively the same impact but not so strong. Transposed to the case of a flame sheet, it effectively shows that the reaction exists only in a fraction of the thermal thickness of the flame (the region close to the flame that the latter preheats, hence, where the reduced temperature rises from 0 to 1 here) where the temperature deviates few from the maximal one (density can be assumed as constant and equal to its burned-gas value). Numerically capturing such a sharp reaction zone can be costly and the lower values of 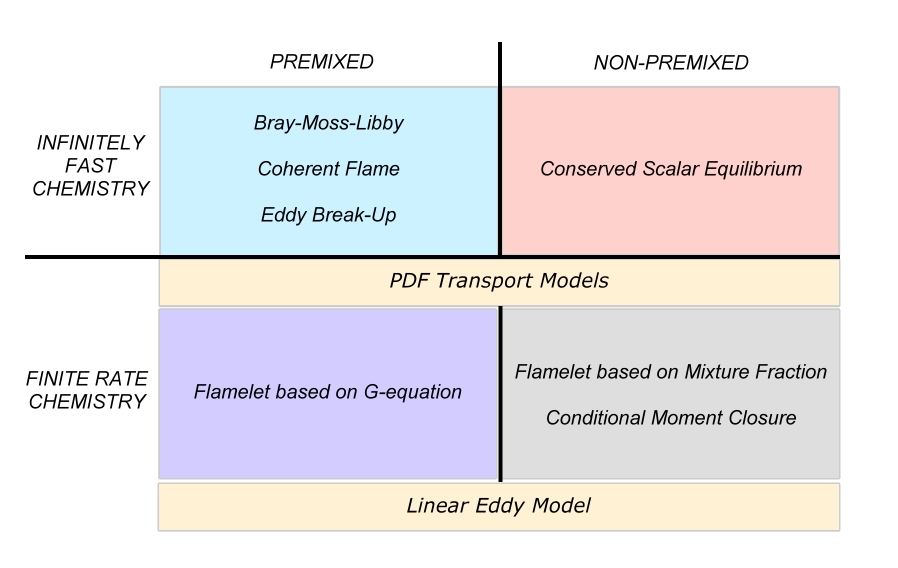

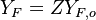 and the oxidizer mass fraction by
and the oxidizer mass fraction by 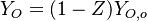 .
. 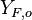 and
and 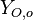 are the fuel and oxidizer mass fractions in the fuel and oxidizer streams, respectively.The mixture fraction posses a transport equation that is expected to not have any source term as a tracer of a mixture must be a conserved scalar. First, the fuel and oxidizer mass fraction transport equations are written in usual notations::
are the fuel and oxidizer mass fractions in the fuel and oxidizer streams, respectively.The mixture fraction posses a transport equation that is expected to not have any source term as a tracer of a mixture must be a conserved scalar. First, the fuel and oxidizer mass fraction transport equations are written in usual notations::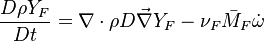 :
: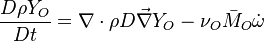 The two above equations are linearly combined in a single one in a manner that the source term disappears::
The two above equations are linearly combined in a single one in a manner that the source term disappears::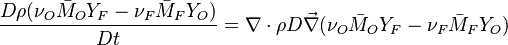 The quantity
The quantity  is thus a conserved scalar. The last step is to normalize it such that it equals unity in the pure fuel stream (
is thus a conserved scalar. The last step is to normalize it such that it equals unity in the pure fuel stream (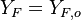 and
and 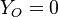 ) and is null in the pure oxidizer stream (
) and is null in the pure oxidizer stream (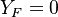 and
and 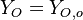 ). The resulting normalized passive scalar is the mixture fraction::
). The resulting normalized passive scalar is the mixture fraction::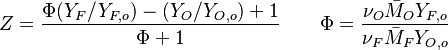 governed by the transport equation:
governed by the transport equation: The stoichiometric interface location (and thus the approximate location of the flame if the flow is reacting) is where
The stoichiometric interface location (and thus the approximate location of the flame if the flow is reacting) is where 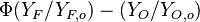 vanishes (or
vanishes (or 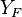 and
and 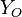 are both null in the reacting case). This leads to a stoichiometry definition::
are both null in the reacting case). This leads to a stoichiometry definition:: As the mixture fraction qualifies the degree of inter-penetration of fuel and oxidizer, the elements originally present in these molecules are conserved and can be directly traced back to the mixture fraction. This has led to an alternate defintion of the mixture fraction, based on element conservation.First, the elemental mass fraction
As the mixture fraction qualifies the degree of inter-penetration of fuel and oxidizer, the elements originally present in these molecules are conserved and can be directly traced back to the mixture fraction. This has led to an alternate defintion of the mixture fraction, based on element conservation.First, the elemental mass fraction  of element j is linked to the species mass fraction
of element j is linked to the species mass fraction 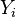 ::
::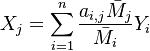 where
where 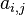 is a matrix counting the number of element j atoms in specie molecule named i and n is the number of species in the mixture.The group pictured by the summation above is a linear combination of
is a matrix counting the number of element j atoms in specie molecule named i and n is the number of species in the mixture.The group pictured by the summation above is a linear combination of  For mass is conserved, the linear combination of the source terms vanishes. Furthermore, by taking the same diffusion coefficient
For mass is conserved, the linear combination of the source terms vanishes. Furthermore, by taking the same diffusion coefficient 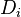 for all the species, the elemental mass fraction transport equation has exactly the same form as the specie transport equation (except the source term). Notice that the assumption of equal diffusion coefficient was also made in the previous definition of the mixture fraction and is justified in turbulent combustion modelling by the turbulence diffusivity flattening the diffusion process in high Reynolds number flows. Hence, the elemental mass fraction transport equation has the same structure as the mixture fraction transport equation seen above. Properly renormalized to reach unity in the fuel stream and zero in the oxidizer stream, the elemental mass fraction is a convenient way of determining the mixture fraction field in a flow. Indeed, it is widely used in practice for this purpose.==== Dissipation Rate ====A very important quantity, derived from the mixture fraction concept, is the scalar dissipation rate, usually noted:
for all the species, the elemental mass fraction transport equation has exactly the same form as the specie transport equation (except the source term). Notice that the assumption of equal diffusion coefficient was also made in the previous definition of the mixture fraction and is justified in turbulent combustion modelling by the turbulence diffusivity flattening the diffusion process in high Reynolds number flows. Hence, the elemental mass fraction transport equation has the same structure as the mixture fraction transport equation seen above. Properly renormalized to reach unity in the fuel stream and zero in the oxidizer stream, the elemental mass fraction is a convenient way of determining the mixture fraction field in a flow. Indeed, it is widely used in practice for this purpose.==== Dissipation Rate ====A very important quantity, derived from the mixture fraction concept, is the scalar dissipation rate, usually noted: 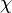 . In the above introduction to non-premixed combustion, it has been said that a diffusion flame is fully controlled through: (i) the position of the stoichiometric line, dictating where the flame sheet lies; (ii) the gradients of fuel on one side and oxidizer on the other side, dictating the feeding rate of the reaction zone through diffusion and thus the strength of combustion. According the the mixture fraction definition, the location of the stoichiometric line is naturally tracked through the
. In the above introduction to non-premixed combustion, it has been said that a diffusion flame is fully controlled through: (i) the position of the stoichiometric line, dictating where the flame sheet lies; (ii) the gradients of fuel on one side and oxidizer on the other side, dictating the feeding rate of the reaction zone through diffusion and thus the strength of combustion. According the the mixture fraction definition, the location of the stoichiometric line is naturally tracked through the 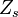 iso-line and it is seen here how the mixture fraction is a convenient tracer to locate the flame.In the same manner, the mixture fraction field should also be able to give information on the strength of the chemistry as the gradients of reactants are directly linked to the mixture fraction distribution. The feeding rate of the reaction zone is characterized through the inverse of a time. Because it is done through diffusion, it must be obtained through a combination of mixture fraction gradient and diffusion coefficient (dimensional analysis)::
iso-line and it is seen here how the mixture fraction is a convenient tracer to locate the flame.In the same manner, the mixture fraction field should also be able to give information on the strength of the chemistry as the gradients of reactants are directly linked to the mixture fraction distribution. The feeding rate of the reaction zone is characterized through the inverse of a time. Because it is done through diffusion, it must be obtained through a combination of mixture fraction gradient and diffusion coefficient (dimensional analysis)::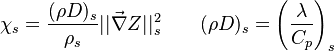 where the subscript s refers to quantities taken effectively where the reacting sheet is supposed to be, close to stoichiometry. This deduction of the scalar dissipation rate, scaling the feeding rate of the flame, is obtained here through physical arguments and is to be derived from equations below in a more mathematical manner. Note that the transport coefficient for the mixture fraction is identified to the one for temperature. This notation is usually used in the literature to emphasize that the rate of temperature diffusion (that is commensurable to the rate of species diffusion) is the retained parameter (as introduced in the following approach highlighting the role of the scalar dissipation rate).Because combustion is highly temperature-dependent, T is certainly the scalar to which attention must be paid for. The temperature equation in the Low-Mach Number regime (
where the subscript s refers to quantities taken effectively where the reacting sheet is supposed to be, close to stoichiometry. This deduction of the scalar dissipation rate, scaling the feeding rate of the flame, is obtained here through physical arguments and is to be derived from equations below in a more mathematical manner. Note that the transport coefficient for the mixture fraction is identified to the one for temperature. This notation is usually used in the literature to emphasize that the rate of temperature diffusion (that is commensurable to the rate of species diffusion) is the retained parameter (as introduced in the following approach highlighting the role of the scalar dissipation rate).Because combustion is highly temperature-dependent, T is certainly the scalar to which attention must be paid for. The temperature equation in the Low-Mach Number regime (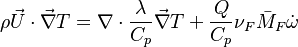 In order to make this equation easily tractable, the Howarth-Dorodnitzyn transform and the Chapman approximation are applied.In the Chapman approximation, the thermal dependence of
In order to make this equation easily tractable, the Howarth-Dorodnitzyn transform and the Chapman approximation are applied.In the Chapman approximation, the thermal dependence of 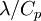 is approximated as
is approximated as 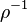 .The Howarth-Dorodnitzyn transform introduces
.The Howarth-Dorodnitzyn transform introduces  in the space coordinate system:
in the space coordinate system:  . The effect of these both mathematical operations is to `digest' the thermal variation of quantities such as density or transport coefficient. Hence, the temperature equation comes in a simpler mathematical shape::
. The effect of these both mathematical operations is to `digest' the thermal variation of quantities such as density or transport coefficient. Hence, the temperature equation comes in a simpler mathematical shape::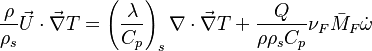 Here the references are taken in the flame, i.e. close to the stoichiometric line (s subscript).In a non-premixed system, strictly speaking,
Here the references are taken in the flame, i.e. close to the stoichiometric line (s subscript).In a non-premixed system, strictly speaking,  , is not really relevant as the flame is fully controlled by the diffusion process. Notwithstanding, in practice, non-premixed flames must be stabilized by creating a strain in the direction of diffusion. This is the reason why the velocity is left in the equation. Because a diffusion flame is fully described by the mixture fraction field, a change in coordinate can be applied::
, is not really relevant as the flame is fully controlled by the diffusion process. Notwithstanding, in practice, non-premixed flames must be stabilized by creating a strain in the direction of diffusion. This is the reason why the velocity is left in the equation. Because a diffusion flame is fully described by the mixture fraction field, a change in coordinate can be applied::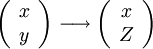 where x is the coordinate tangential to the iso-
where x is the coordinate tangential to the iso-![\left [\begin{array}{cc}\frac{\partial x}{\partial x} & \frac{\partial Z}{\partial x} \\\frac{\partial x}{\partial y} & \frac{\partial Z}{\partial y} \end{array}\right ] = \left [\begin{array}{cc}1 & 0 \\0 & l_d^{-1} \end{array}\right ]](/W/images/math/c/f/3/cf33ed5db4bbe31f9f26bc2a389440c2.png) Note that the diffusive layer of thickness
Note that the diffusive layer of thickness 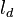 is defined as the region of transition between fuel and oxidizer and is thus given by the gradient of Z along the y direction.This transform is applied to the vectorial operators::
is defined as the region of transition between fuel and oxidizer and is thus given by the gradient of Z along the y direction.This transform is applied to the vectorial operators::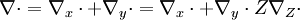 :
: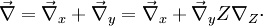 With this transform, the above temperature equation looks like::
With this transform, the above temperature equation looks like::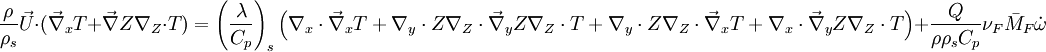 As mentioned above, the velocity and the variation along the tangential direction to the main flame structure x are not supposed to play a major role. By emphasizing the role of the gradient of Z along y as a key parameter defining the configuration the following equation is obtained::
As mentioned above, the velocity and the variation along the tangential direction to the main flame structure x are not supposed to play a major role. By emphasizing the role of the gradient of Z along y as a key parameter defining the configuration the following equation is obtained::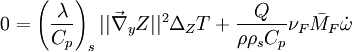 This equation (sometimes named the flamelet equation) serves as the basic framework to study the structure of diffusion flames. It highlights the role of the dissipation rate with respect to the strength of the source term and shows that the dissipation rate calibrates the combustion intensity.To describe the structure of the diffusion flame, the reduced mixture fraction is set::
This equation (sometimes named the flamelet equation) serves as the basic framework to study the structure of diffusion flames. It highlights the role of the dissipation rate with respect to the strength of the source term and shows that the dissipation rate calibrates the combustion intensity.To describe the structure of the diffusion flame, the reduced mixture fraction is set::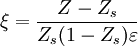 The utility of the reduced mixture fraction is to focus on the reaction zone. This reaction zone is supposed located on the stoichiometric line (this is why the reduced mixture fraction is centred on
The utility of the reduced mixture fraction is to focus on the reaction zone. This reaction zone is supposed located on the stoichiometric line (this is why the reduced mixture fraction is centred on  ).== The Premixed Regime ==
).== The Premixed Regime ==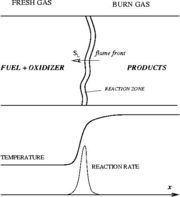
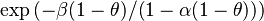 of the reaction source upstream in the fresh gas (
of the reaction source upstream in the fresh gas ( ) and in the reaction zone close to equilibrium temperature (
) and in the reaction zone close to equilibrium temperature ( ) for the set of representative values:
) for the set of representative values: 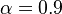 . It is found that the reaction is about
. It is found that the reaction is about  times slower in the freshgas than close to the burned gas. It is known that the chemical time scale is about 0.1 ms in the reaction zone of a typical flame, then the typical reaction time in the fresh gas in normal conditions is about
times slower in the freshgas than close to the burned gas. It is known that the chemical time scale is about 0.1 ms in the reaction zone of a typical flame, then the typical reaction time in the fresh gas in normal conditions is about 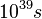 . To be compared with the order of magnitude of the estimated Universe age:
. To be compared with the order of magnitude of the estimated Universe age: 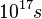 . Non-negligible chemistry is only confined in a thin reaction zone stuck to the hot burned gas at equilibrium temperature. In this zone, the
. Non-negligible chemistry is only confined in a thin reaction zone stuck to the hot burned gas at equilibrium temperature. In this zone, the 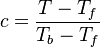 It is seen that c is a normalization of a scalar quantity. As mentioned above, the scalar transport equations are assumed linear such that the transport equation for c can be obtained directly. Actually, the transport equation for T (
It is seen that c is a normalization of a scalar quantity. As mentioned above, the scalar transport equations are assumed linear such that the transport equation for c can be obtained directly. Actually, the transport equation for T (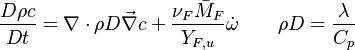 The fact that the default or excess of fuel has been discussed above leads to the introduction of another quantity: the equivalence ratio. The equivalence ratio, usually noted
The fact that the default or excess of fuel has been discussed above leads to the introduction of another quantity: the equivalence ratio. The equivalence ratio, usually noted 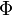 , is the ratio of two ratios. The first one is the ratio of the mass of fuel with the mass of oxidizer in the mixture. The second one is the same ratio for a mixture at stoichiometry. Hence, when the equivalence ratio equals unity, the mixture is at stoichiometry. If it is greater than unity, the mixture is named rich as there is an excess of fuel. In contrast, when it is smaller than unity the mixture is named lean. The equivalence ratio presented here for premixed flames has little connection with the equivalence ratio introduced earlier regarding the non-premixed regime. Basically, the equivalence ratio as defined for non-premixed flames gives the equivalence ratio of a premixed mixture with the same mass of fuel and oxidizer. Moreover, the equivalence ratio as defined for a premixed mixture can be obtained based on the mixture fraction (it is thus the local equivalence ratio at a point in the non-homogeneous mixture described by the mixture fraction). From the definitions given above::
, is the ratio of two ratios. The first one is the ratio of the mass of fuel with the mass of oxidizer in the mixture. The second one is the same ratio for a mixture at stoichiometry. Hence, when the equivalence ratio equals unity, the mixture is at stoichiometry. If it is greater than unity, the mixture is named rich as there is an excess of fuel. In contrast, when it is smaller than unity the mixture is named lean. The equivalence ratio presented here for premixed flames has little connection with the equivalence ratio introduced earlier regarding the non-premixed regime. Basically, the equivalence ratio as defined for non-premixed flames gives the equivalence ratio of a premixed mixture with the same mass of fuel and oxidizer. Moreover, the equivalence ratio as defined for a premixed mixture can be obtained based on the mixture fraction (it is thus the local equivalence ratio at a point in the non-homogeneous mixture described by the mixture fraction). From the definitions given above:: ==== Premixed Flame Péclet Number ====Earlier in this section, it has been said that a premixed flame posses its own dynamics, as a free propagating surface, and has thus characteristic quantities. For this reason, a Péclet number may be defined, based on these quantities. The Péclet number has the same structure as the Reynolds number but the dynamical viscosity is replaced by the ratio of the thermal conductivity and the heat capacity of the mixture. The thickness
==== Premixed Flame Péclet Number ====Earlier in this section, it has been said that a premixed flame posses its own dynamics, as a free propagating surface, and has thus characteristic quantities. For this reason, a Péclet number may be defined, based on these quantities. The Péclet number has the same structure as the Reynolds number but the dynamical viscosity is replaced by the ratio of the thermal conductivity and the heat capacity of the mixture. The thickness 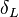 of a premixed flame is essentially thermal. It means that it corresponds to the distance of the temperature rise between fresh and burned gases. This thickness is below the millimetre for conventional flames. The width of the reaction zone inside this flame is even smaller, by about one order of magnitude. This reaction zone is stuck to the hot side of the flame due to the high thermal dependency of the combustion reactions, as seen above. Hence, the flame region is essentially governed by a convection-diffusion process, the source term being negligible in most of it.It is convenient to write the progress variable transport equation in a steady-state framework. The quantities at flame temperature (
of a premixed flame is essentially thermal. It means that it corresponds to the distance of the temperature rise between fresh and burned gases. This thickness is below the millimetre for conventional flames. The width of the reaction zone inside this flame is even smaller, by about one order of magnitude. This reaction zone is stuck to the hot side of the flame due to the high thermal dependency of the combustion reactions, as seen above. Hence, the flame region is essentially governed by a convection-diffusion process, the source term being negligible in most of it.It is convenient to write the progress variable transport equation in a steady-state framework. The quantities at flame temperature (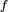 ) are used to non-dimensionalize the equation::
) are used to non-dimensionalize the equation::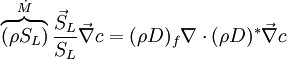 Note that the source term is neglected, consistently with what has been said above.This convection-diffusion equation makes appear a first approximation of a flame Péclet number::
Note that the source term is neglected, consistently with what has been said above.This convection-diffusion equation makes appear a first approximation of a flame Péclet number::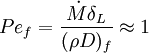 From the Péclet number, it is possible to obtain an expression for the flame velocity (remembering that
From the Péclet number, it is possible to obtain an expression for the flame velocity (remembering that 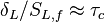 , vid. inf.
, vid. inf. 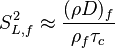 For typical hydrocarbon flames, the speed is some tens of centimetres per second and the diffusivity is some
For typical hydrocarbon flames, the speed is some tens of centimetres per second and the diffusivity is some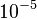 square metres per second. The chemical time in the reaction zone of about one tenth of a millisecond is recovered.==== Details of the Premixed Unstrained Planar Flame ====A plane combustion wave propagating in a homogeneous fresh mixture is the reference case to describe the premixed regime. At constant speed, it is convenient to see the flame at rest with a flowing upstream mixture. This is actually the way propagating flames are usually stabilized. In the frame of description, the physics is 1-D, steady with a uniform (the flame is said unstrained) mass flowing across the system. Two types of equations are thus sufficient to describe the problem, the temperature transport equation and the species transport equations, as in
square metres per second. The chemical time in the reaction zone of about one tenth of a millisecond is recovered.==== Details of the Premixed Unstrained Planar Flame ====A plane combustion wave propagating in a homogeneous fresh mixture is the reference case to describe the premixed regime. At constant speed, it is convenient to see the flame at rest with a flowing upstream mixture. This is actually the way propagating flames are usually stabilized. In the frame of description, the physics is 1-D, steady with a uniform (the flame is said unstrained) mass flowing across the system. Two types of equations are thus sufficient to describe the problem, the temperature transport equation and the species transport equations, as in 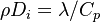 (unity Lewis numbers). Suppose the 1-D domain is described thanks to a conventional (Ox) axis with a flame propagating towards negative x (this is the conventional usage), the boundary conditions are::* in the frozen mixture: :**
(unity Lewis numbers). Suppose the 1-D domain is described thanks to a conventional (Ox) axis with a flame propagating towards negative x (this is the conventional usage), the boundary conditions are::* in the frozen mixture: :** 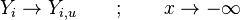 :**
:** 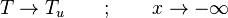 :* in the burned gas region supposed at equilibrium::**
:* in the burned gas region supposed at equilibrium::**  :**
:** 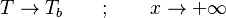 :
: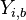 and
and 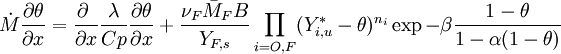 This equation is further simplified by the variable change
This equation is further simplified by the variable change 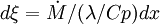 ::
::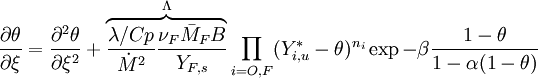 == The Partially-Premixed Regime ==
== The Partially-Premixed Regime ==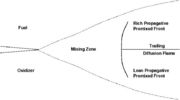
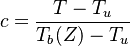 = Three Turbulent-Flame Interaction Regimes =It may appear odd to try to describe here what is the reason of combustion modelling research: the interaction of the turbulence with chemistry. However, one of the first steps in building knowledge in turbulent combustion was the qualitative exploration of what might be the dynamics of a flame in a turbulent environment. This led to what is now known as combustion diagrams. As explained above, the premixed regime lends itself the easiest to such an approach as it exhibits natural intrinsic quantities which are not as objectively identifiable in the other combustion regimes. Note that these quantities may dependon the geometry of the flame: for instance turbulence can bend a flame sheet, leading to a change in its dynamics compared to the flat flame propagating in a medium at rest. In this section, the turbulence-flame interaction modes will be described for a premixed flame. Only remarks will be added regarding the non-premixed and partially-premixed regimes.An integral quantity to assess the interaction between a premixed flame sheet and the turbulenceis the Karlovitz number Ka. It compares the characteristic time of flame displacement with the characteristic time of the smallest structures (that are also the fastest) of the turbulence.:
= Three Turbulent-Flame Interaction Regimes =It may appear odd to try to describe here what is the reason of combustion modelling research: the interaction of the turbulence with chemistry. However, one of the first steps in building knowledge in turbulent combustion was the qualitative exploration of what might be the dynamics of a flame in a turbulent environment. This led to what is now known as combustion diagrams. As explained above, the premixed regime lends itself the easiest to such an approach as it exhibits natural intrinsic quantities which are not as objectively identifiable in the other combustion regimes. Note that these quantities may dependon the geometry of the flame: for instance turbulence can bend a flame sheet, leading to a change in its dynamics compared to the flat flame propagating in a medium at rest. In this section, the turbulence-flame interaction modes will be described for a premixed flame. Only remarks will be added regarding the non-premixed and partially-premixed regimes.An integral quantity to assess the interaction between a premixed flame sheet and the turbulenceis the Karlovitz number Ka. It compares the characteristic time of flame displacement with the characteristic time of the smallest structures (that are also the fastest) of the turbulence.: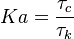
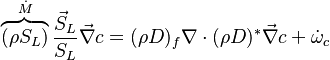 The premixed wave propagates at a speed
The premixed wave propagates at a speed 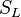 because it is fed by reactants diffusing inside the combustion zone and which are preheated because temperature diffuses in the reverse direction. The speed at which the flame progresses is thus related to the rate of species diffusion into the reaction zone which are then consumed. As the premixed flame is a free propagating wave whose speed of propagation is only limited by the chemical strength, the characteristic chemical time is based only on the diffusion and the mass flow rate experienced by the flame::
because it is fed by reactants diffusing inside the combustion zone and which are preheated because temperature diffuses in the reverse direction. The speed at which the flame progresses is thus related to the rate of species diffusion into the reaction zone which are then consumed. As the premixed flame is a free propagating wave whose speed of propagation is only limited by the chemical strength, the characteristic chemical time is based only on the diffusion and the mass flow rate experienced by the flame::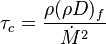 The smallest eddies are the ones being dissipated by the viscous forces. Their characteristic time is estimated thanks to a combination of the viscosity and the flux of turbulent energy to be dissipated (also called turbulent dissipation
The smallest eddies are the ones being dissipated by the viscous forces. Their characteristic time is estimated thanks to a combination of the viscosity and the flux of turbulent energy to be dissipated (also called turbulent dissipation 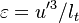 )::
)::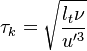 Thanks to those definitions of chemical and small structure times, it is possible to give another definition of the Karlovitz number::
Thanks to those definitions of chemical and small structure times, it is possible to give another definition of the Karlovitz number::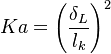 which is the square of the ratio between the premixed flame thickness and the small structure scale: Ka actually compares scales. To arrive to this latter result, the three following assumptions must be used: (i) the flame thickness is obtained thanks to the premixed flame Péclet number (vid. sup.); (ii) the turbulence small structure (Kolmogorov eddies) scale is given by:
which is the square of the ratio between the premixed flame thickness and the small structure scale: Ka actually compares scales. To arrive to this latter result, the three following assumptions must be used: (i) the flame thickness is obtained thanks to the premixed flame Péclet number (vid. sup.); (ii) the turbulence small structure (Kolmogorov eddies) scale is given by: 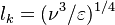 following the same dimensional argument as for the estimation of its time; and (iii) scalar diffusion scales with viscosity. ==== Remark Regarding the Diffusion Flame ====From what has been presented above, a diffusion flame does not have characteristic scales. Setting a turbulence combustion regime classification for non-premixed flames has still not been answered by research. Some laws of behaviour will only be drawn around the scalar dissipation rate which is the parameter of integral importance for a diffusion flame.Indeed, the dynamics of a diffusion flame is determined by the strain rate imposed by the turbulence. As for the premixed flames, the shortest eddies (Kolmogorov) are the ones having the largest impact. The diffusive layer is thus given by the size of the Kolmogrov eddies:
following the same dimensional argument as for the estimation of its time; and (iii) scalar diffusion scales with viscosity. ==== Remark Regarding the Diffusion Flame ====From what has been presented above, a diffusion flame does not have characteristic scales. Setting a turbulence combustion regime classification for non-premixed flames has still not been answered by research. Some laws of behaviour will only be drawn around the scalar dissipation rate which is the parameter of integral importance for a diffusion flame.Indeed, the dynamics of a diffusion flame is determined by the strain rate imposed by the turbulence. As for the premixed flames, the shortest eddies (Kolmogorov) are the ones having the largest impact. The diffusive layer is thus given by the size of the Kolmogrov eddies:  and the typical diffusion time scale (feeding rate of the reaction zone) is given by the characteristic time of the Kolmogorov eddies:
and the typical diffusion time scale (feeding rate of the reaction zone) is given by the characteristic time of the Kolmogorov eddies:  as the Reynolds number of the Kolmogorov structures is unity. Here,
as the Reynolds number of the Kolmogorov structures is unity. Here, 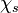 is the sample-averaging of
is the sample-averaging of 
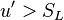 . In that case, although the flame structure is not altered by the small structures, it can be convected by large structures such that areas of different locations in the front interact. It shows that, even with a small Karlovitz number, the turbulence effect is not always weak.== The Corrugated Regime ==
. In that case, although the flame structure is not altered by the small structures, it can be convected by large structures such that areas of different locations in the front interact. It shows that, even with a small Karlovitz number, the turbulence effect is not always weak.== The Corrugated Regime ==
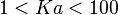 , the laminar structure of the reaction zone is still preserved but not the one of the preheat zone.== The Thickened Regime ==
, the laminar structure of the reaction zone is still preserved but not the one of the preheat zone.== The Thickened Regime ==
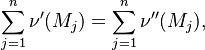
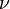 denotes the stoichiometric coefficient, and
denotes the stoichiometric coefficient, and 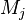 stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction. The reaction rate, expressing the rate of disappearance of reactant i, is defined as:
stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction. The reaction rate, expressing the rate of disappearance of reactant i, is defined as: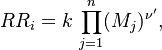

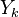 of k-th species is:
of k-th species is: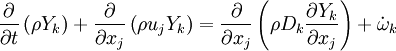 where Ficks' law is assumed for scalar diffusion with
where Ficks' law is assumed for scalar diffusion with  denoting the species difussion coefficient, and
denoting the species difussion coefficient, and  denoting the species reaction rate.A non-reactive (passive) scalar (like the mixture fraction
denoting the species reaction rate.A non-reactive (passive) scalar (like the mixture fraction  ) is goverened by the following transport equation:
) is goverened by the following transport equation: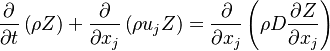 where
where 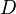 is the diffusion coefficient of the passive scalar.=== RANS equations ===In turbulent flows,
is the diffusion coefficient of the passive scalar.=== RANS equations ===In turbulent flows, 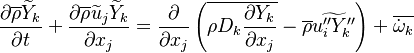 where the turbulent fluxes
where the turbulent fluxes 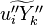 and reaction terms
and reaction terms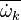 need to be closed.The passive scalar turbulent transport equation is:
need to be closed.The passive scalar turbulent transport equation is: where
where 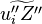 needs modelling. A common practice is to model the turbulent fluxes using the gradient diffusion hypothesis. For example, in the equation above the flux
needs modelling. A common practice is to model the turbulent fluxes using the gradient diffusion hypothesis. For example, in the equation above the flux 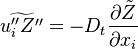 where
where 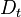 is the turbulent diffusivity. Since
is the turbulent diffusivity. Since 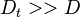 , the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.In addition to the mean passive scalar equation,an equation for the Favre variance
, the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.In addition to the mean passive scalar equation,an equation for the Favre variance 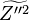 is often employed:
is often employed: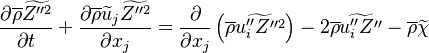 where
where  is the mean
is the mean 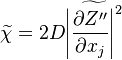 This term and the variance diffusion fluxes needs to be modelled.=== LES equations ===The
This term and the variance diffusion fluxes needs to be modelled.=== LES equations ===The  where
where  is the transport of subgrid fluctuations of mass fraction:
is the transport of subgrid fluctuations of mass fraction: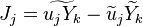 and has to be modelled.Fluctuations of diffusion coefficients are often ignored and their contributionsare assumed to be much smaller than the apparent turbulent diffusion due to transport of subgrid fluctuations.The first term on the right hand side is then:
and has to be modelled.Fluctuations of diffusion coefficients are often ignored and their contributionsare assumed to be much smaller than the apparent turbulent diffusion due to transport of subgrid fluctuations.The first term on the right hand side is then: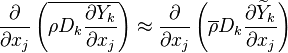 == Infinitely fast chemistry ==All combustion models can be divided into two main groups according to the assumptions on the reaction kinetics.We can either assume the reactions to be infinitely fast - compared to e.g. mixing of the species, or comparable to the time scale of the mixing process. The simple approach is to assume infinitely fast chemistry. Historically, mixing of the species is the older approach, and it is still in wide use today. It is therefore simpler to solve for
== Infinitely fast chemistry ==All combustion models can be divided into two main groups according to the assumptions on the reaction kinetics.We can either assume the reactions to be infinitely fast - compared to e.g. mixing of the species, or comparable to the time scale of the mixing process. The simple approach is to assume infinitely fast chemistry. Historically, mixing of the species is the older approach, and it is still in wide use today. It is therefore simpler to solve for 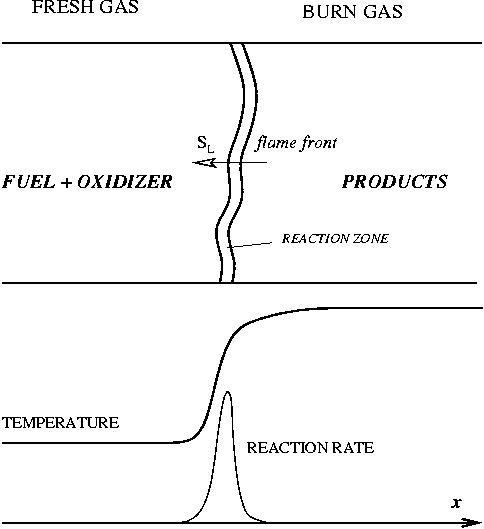
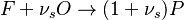
![\bar{\dot\omega}_F=A_{EB} \frac{\epsilon}{k} min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu},B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right]](/W/images/math/9/d/6/9d67c48a8dd1f2decb0d5bf3336d215b.png)
 denotes the mean concentrations of fuel, oxidiser, and products respectively. A and B are model constants with typical values of 0.5 and 4.0 respectively. The values of these constants are fitted according to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for all the situations. Care must be taken especially in highly strained regions, where the ratio of
denotes the mean concentrations of fuel, oxidiser, and products respectively. A and B are model constants with typical values of 0.5 and 4.0 respectively. The values of these constants are fitted according to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for all the situations. Care must be taken especially in highly strained regions, where the ratio of 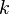 to
to  is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.CFD codes usually have some remedies to overcome this problem.This model largely over-predicts temperatures and concentrations of species like CO and other species. However, the Eddy Break-Up model enjoys a popularity for its simplicity, steady convergence, and implementation.==== Bray-Moss-Libby model ======= Non-premixed combustion ===Non premixed combustion is a special class of combustion where fuel and oxidizerenter separately into the combustion chamber. The diffusion and mixing of the two streamsmust bring the reactants together for the reaction to occur.Mixing becomes the key characteristic for diffusion flames.Diffusion burners are easier and safer to operate than premixed burners.However their efficiency is reduced compared to premixed burners.One of the major theoretical tools in non-premixed combustionis the passive scalar
is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.CFD codes usually have some remedies to overcome this problem.This model largely over-predicts temperatures and concentrations of species like CO and other species. However, the Eddy Break-Up model enjoys a popularity for its simplicity, steady convergence, and implementation.==== Bray-Moss-Libby model ======= Non-premixed combustion ===Non premixed combustion is a special class of combustion where fuel and oxidizerenter separately into the combustion chamber. The diffusion and mixing of the two streamsmust bring the reactants together for the reaction to occur.Mixing becomes the key characteristic for diffusion flames.Diffusion burners are easier and safer to operate than premixed burners.However their efficiency is reduced compared to premixed burners.One of the major theoretical tools in non-premixed combustionis the passive scalar 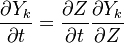
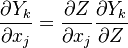 and transformation :
and transformation :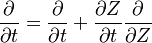 upon substitution into the species transport equation (see
upon substitution into the species transport equation (see ![\rho \frac{\partial Y_k}{\partial t} + Y_k \left[\frac{\partial \rho}{\partial t} + \frac{\partial \rho u_j}{\partial x_j}\right]+ \frac{\partial Y_k}{\partial Z} \left[ \rho \frac{\partial Z}{\partial t} + \rho u_j \frac{\partial Z}{\partial x_j} -\frac{\partial}{\partial x_j}\left( \rho D \frac{\partial Z}{\partial x_j} \right)\right]=\rho D \left( \frac{\partial Z}{\partial x_j} \frac{\partial Z}{\partial x_j} \right)\frac{\partial^2 Y_k}{\partial Z^2} + \dot \omega_k](/W/images/math/7/6/9/76972aa831910042bbf0ce5e9610a31b.png) The second and third terms in the LHS cancel out due to continuity and mixture fraction transport.At the outset, the equation boils down to:
The second and third terms in the LHS cancel out due to continuity and mixture fraction transport.At the outset, the equation boils down to: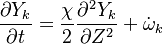 where
where 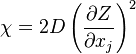 is called the scalar dissipationwhich controls the mixing, providing the interaction between the flow and the chemistry.If the flame dependence on time is dropped, even though the field
is called the scalar dissipationwhich controls the mixing, providing the interaction between the flow and the chemistry.If the flame dependence on time is dropped, even though the field 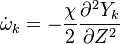 If the reaction is assumed to be infinetly fast, the resultant flame distribution is in equilibrium.and
If the reaction is assumed to be infinetly fast, the resultant flame distribution is in equilibrium.and  . When the flame is in equilibrium, the flame configuration
. When the flame is in equilibrium, the flame configuration 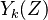 is independent of strain.===== Burke-Schumann flame structure =====The Burke-Schuman solution is valid for irreversible infinitely fast chemistry.With a reaction in the form of
is independent of strain.===== Burke-Schumann flame structure =====The Burke-Schuman solution is valid for irreversible infinitely fast chemistry.With a reaction in the form of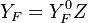 Oxidizer mass fraction:
Oxidizer mass fraction: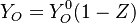 Where
Where  and
and  are fuel and oxidizer mass fractionsin the pure fuel and oxidizer streams respectively.The other solution is given by a discontinuous slope at stoichiometric mixture fraction
are fuel and oxidizer mass fractionsin the pure fuel and oxidizer streams respectively.The other solution is given by a discontinuous slope at stoichiometric mixture fraction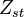 and two linear profiles (in the rich and lean side) at eitherside of the stoichiometric mixture fraction.Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.:
and two linear profiles (in the rich and lean side) at eitherside of the stoichiometric mixture fraction.Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.: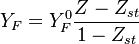 and oxidizer mass fraction:
and oxidizer mass fraction: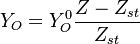 == Finite rate chemistry ===== Premixed combustion ======= Coherent flame model ======== Flamelets based on G-equation ======== Flame surface density model ======= Non-premixed combustion ======= Flamelets based on conserved scalar ====Peters (2000) define Flamelets as "thin diffusion layers embedded in a turbulent non-reactive flow field".If the chemistry is fast enough, the chemistry is active within a thin regionwhere the chemistry conditions are in (or close to) stoichiometric conditions, the "flame" surface.This thin region is assumed to be smaller than Kolmogorov length scale and therefore theregion is locally laminar. The flame surface is defined as an iso-surface of a certain scalar
== Finite rate chemistry ===== Premixed combustion ======= Coherent flame model ======== Flamelets based on G-equation ======== Flame surface density model ======= Non-premixed combustion ======= Flamelets based on conserved scalar ====Peters (2000) define Flamelets as "thin diffusion layers embedded in a turbulent non-reactive flow field".If the chemistry is fast enough, the chemistry is active within a thin regionwhere the chemistry conditions are in (or close to) stoichiometric conditions, the "flame" surface.This thin region is assumed to be smaller than Kolmogorov length scale and therefore theregion is locally laminar. The flame surface is defined as an iso-surface of a certain scalar 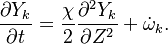 This approach is called the Stationary Laminar Flamelet Model (SLFM) and has the advantage thatflamelet profiles
This approach is called the Stationary Laminar Flamelet Model (SLFM) and has the advantage thatflamelet profiles 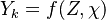 can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory
can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory 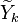 .In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scaleand obviously is much smaller than the grid size.It is therefore needed a distribution of the passive scalar within the cell.
.In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scaleand obviously is much smaller than the grid size.It is therefore needed a distribution of the passive scalar within the cell. , where
, where 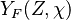 correspondsto the value obtained from the flamelets libraries.A generic solution can be expressed as:
correspondsto the value obtained from the flamelets libraries.A generic solution can be expressed as: where
where 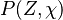 is the joint
is the joint 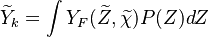
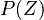 is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a
is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a 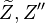 .If the mixture fraction and scalar dissipation are consider independent variables,
.If the mixture fraction and scalar dissipation are consider independent variables, . The PDF of the scalar dissipation is assumed to be log-normal withvariance unity.:
. The PDF of the scalar dissipation is assumed to be log-normal withvariance unity.: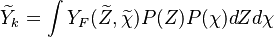 In
In 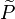 .The same equation hold by replacing averaged values with filtered values.:
.The same equation hold by replacing averaged values with filtered values.: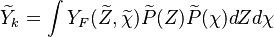 The assumptions made regarding the shapes of the PDFs are still justified. In LES combustion the
The assumptions made regarding the shapes of the PDFs are still justified. In LES combustion the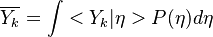 where
where  is the sample space for
is the sample space for 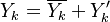 The fluctuations
The fluctuations 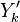 are usually very strong in time and space which makes the closureof
are usually very strong in time and space which makes the closureof 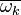 very difficult.However, the alternative decomposition:
very difficult.However, the alternative decomposition: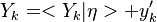 where
where 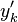 is the fluctuation around the conditional mean or the "conditional fluctuation".Experimentally, it is observed that
is the fluctuation around the conditional mean or the "conditional fluctuation".Experimentally, it is observed that 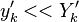 , which forms the basic assumption of the CMC method.Closures. Due to this property better closure methods can be used reducing the non-linearity of the mass fraction equations.The
, which forms the basic assumption of the CMC method.Closures. Due to this property better closure methods can be used reducing the non-linearity of the mass fraction equations.The  for simplicity.:
for simplicity.: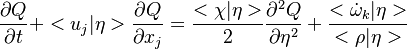 In this equation, high order terms in Reynolds number have been neglected.(See
In this equation, high order terms in Reynolds number have been neglected.(See  ) will give rise to large errors.However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.The first order closure
) will give rise to large errors.However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.The first order closure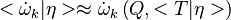 is a good approximation in zones which are not close to extinction.===== Second order closure =====A second order closure can be obtained if conditional fluctuations are taken into account.For a chemical source term in the form
is a good approximation in zones which are not close to extinction.===== Second order closure =====A second order closure can be obtained if conditional fluctuations are taken into account.For a chemical source term in the form 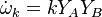 with the rate constant in Arrhenius form
with the rate constant in Arrhenius form![k=A_0 T^\beta exp [-Ta/T]](/W/images/math/2/e/0/2e0c186caff5787cd5f2f76baac86531.png) the second order closure is (Klimenko and Bilger 1999):
the second order closure is (Klimenko and Bilger 1999):![< \dot \omega_k|\eta> \approx < \dot \omega_k|\eta >^{FO}\left[1+ \frac{< Y''_A Y''_B |\eta>}{Q_A Q_B}+ \left( \beta + T_a/Q_T \right)\left(\frac{< Y''_A T'' |\eta>}{Q_AQ_T} + \frac{< Y''_B T'' |\eta>}{Q_BQ_T}\right) + ... \right]](/W/images/math/f/9/c/f9c779360789a63c6bb68e8c13d0489a.png) where
where  is the first order CMC closure and
is the first order CMC closure and .When the temperature exponent
.When the temperature exponent  are large the error of taking the first order approximation increases.Improvement of small pollutant predictions can be obtained using the above reaction rate for selected species like CO and NO.===== Double conditioning =====Close to extinction and reignition. The conditional fluctuations can be very largeand the primary closure of CMC of "small" fluctuations is not longer valid.A second variable
are large the error of taking the first order approximation increases.Improvement of small pollutant predictions can be obtained using the above reaction rate for selected species like CO and NO.===== Double conditioning =====Close to extinction and reignition. The conditional fluctuations can be very largeand the primary closure of CMC of "small" fluctuations is not longer valid.A second variable 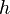 can be chosen to define a double conditioned mass fraction:
can be chosen to define a double conditioned mass fraction: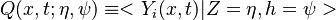 Due to the strong dependence on chemical reactions to temperature,
Due to the strong dependence on chemical reactions to temperature,  therefore represents a conditionally filtered reactive scalar.=== Linear Eddy Model ===The Linear Eddy Model (LEM) was first developed by Kerstein(1988).It is an one-dimensional model for representing the flame structure in turbulent flows.In every computational cell a molecular, diffusion and chemical model is defined as:
therefore represents a conditionally filtered reactive scalar.=== Linear Eddy Model ===The Linear Eddy Model (LEM) was first developed by Kerstein(1988).It is an one-dimensional model for representing the flame structure in turbulent flows.In every computational cell a molecular, diffusion and chemical model is defined as: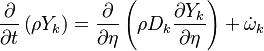 where
where 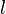 , smaller than the grid size at a location
, smaller than the grid size at a location 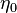 within the one-dimensional domain. This vortex distort the
within the one-dimensional domain. This vortex distort the 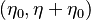 .The vortex size
.The vortex size 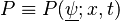 where
where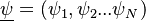 is the phase space for the reactive scalars
is the phase space for the reactive scalars .The transport equation of the joint PDF is::
.The transport equation of the joint PDF is::![\frac{\partial <\rho | \underline{Y}=\underline{\psi}> P }{\partial t} + \frac{ \partial <\rho u_j | \underline{Y}=\underline{\psi}> P }{\partial x_j} =\sum^N_\alpha \frac{\partial}{\partial \psi_\alpha}\left[ \rho \dot{\omega}_\alpha P \right]- \sum^N_\alpha \sum^N_\beta \frac{\partial^2}{\partial \psi_\alpha \psi_\beta}\left[ <D \frac{\partial Y_\alpha}{\partial x_i} \frac{\partial Y_\beta}{\partial x_i} | \underline{Y}=\underline{\psi}> \right] P](/W/images/math/1/3/7/13767f4c5947b8df82fdd84c944ea62b.png) where the chemical source term is closed. Another term appeared on the right hand side which accounts for the effects ofthe molecular mixing on the PDF, is the so called "micro-mixing " term.Equal diffusivities are used for simplicity
where the chemical source term is closed. Another term appeared on the right hand side which accounts for the effects ofthe molecular mixing on the PDF, is the so called "micro-mixing " term.Equal diffusivities are used for simplicity  A more general approach is the velocity-composition joint-PDFwith
A more general approach is the velocity-composition joint-PDFwith 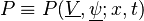 , where
, where 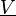 is the sample space of the velocity field
is the sample space of the velocity field 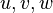 . This approach has the advantage of avoiding gradient-diffusionmodelling. A similar equation to the above is obtained combining the momentum and scalar transport equation.The PDF transport equation can be solved in two ways: through a Lagrangian approachusing stochastic methods or in a Eulerian ways using stochastic fields.==== Lagrangian ====The main idea of Lagrangian methods is that the flow can be represented by an ensemble of fluid particles. Central to this approach is the stochastic differential equations and in particular the
. This approach has the advantage of avoiding gradient-diffusionmodelling. A similar equation to the above is obtained combining the momentum and scalar transport equation.The PDF transport equation can be solved in two ways: through a Lagrangian approachusing stochastic methods or in a Eulerian ways using stochastic fields.==== Lagrangian ====The main idea of Lagrangian methods is that the flow can be represented by an ensemble of fluid particles. Central to this approach is the stochastic differential equations and in particular the 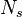 scalar variables(the stochastic field
scalar variables(the stochastic field 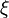 ) is used to represent thePDF:
) is used to represent thePDF:![P (\underline{\psi}; x,t) = \frac{1}{N} \sum^{N_s}_{j=1} \prod^{N}_{k=1} \delta \left[\psi_k -\xi_k^j(x,t) \right]](/W/images/math/f/2/3/f23f3d712f59f83ab17babbfbe9834ab.png) ===Other combustion models======= MMC ====The Multiple Mapping Conditioning (MMC) (Klimenko and Pope 2003) is anextension of the
===Other combustion models======= MMC ====The Multiple Mapping Conditioning (MMC) (Klimenko and Pope 2003) is anextension of the