NACA0012 airfoil
From CFD-Wiki
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
The NACA 0012 airfoil is widely used. The simple geometry and the large amount of wind tunnel data provide an excellent 2D validation case. For this case I use the Spalart-Allmaras turbulence model. | The NACA 0012 airfoil is widely used. The simple geometry and the large amount of wind tunnel data provide an excellent 2D validation case. For this case I use the Spalart-Allmaras turbulence model. | ||
| - | |||
| - | |||
<br> | <br> | ||
| + | == Mesh == | ||
| + | |||
[[Image:Naca0012 mesh final.JPG]] | [[Image:Naca0012 mesh final.JPG]] | ||
<br><br> | <br><br> | ||
The mesh is a 30,000 cell C-grid. The width off the first cell at the foil boundary is 0.02 mm. At Re = 3e6 this results in a wall y+ = 1.3 ± 0.4 . The mesh shown is for an Angle of Attack of 6 degrees. | The mesh is a 30,000 cell C-grid. The width off the first cell at the foil boundary is 0.02 mm. At Re = 3e6 this results in a wall y+ = 1.3 ± 0.4 . The mesh shown is for an Angle of Attack of 6 degrees. | ||
| - | |||
| - | |||
<br> | <br> | ||
| + | == Drag Coefficient == | ||
| + | |||
[[Image:Naca0012 cd tripwire.JPG]] | [[Image:Naca0012 cd tripwire.JPG]] | ||
<br><br> | <br><br> | ||
The drag coefficient at zero Angle of Attack depends on the Reynold's number. The experimental data is for an airfoil with a trip wire that forces the experimental boundary layer to be completely turbulent.[1] This corresponds to the Fluent model, which has an active turbulence model over the complete airfoil. | The drag coefficient at zero Angle of Attack depends on the Reynold's number. The experimental data is for an airfoil with a trip wire that forces the experimental boundary layer to be completely turbulent.[1] This corresponds to the Fluent model, which has an active turbulence model over the complete airfoil. | ||
| - | |||
| - | |||
<br> | <br> | ||
| + | == Lift Curve == | ||
| + | |||
[[Image:Naca0012 lift curve.JPG]] | [[Image:Naca0012 lift curve.JPG]] | ||
<br><br> | <br><br> | ||
The lift coefficient depends on the Angle of Attack. For Re = 2e6 I compare the lift coefficient to experimental results.[2] | The lift coefficient depends on the Angle of Attack. For Re = 2e6 I compare the lift coefficient to experimental results.[2] | ||
| - | |||
| - | |||
<br> | <br> | ||
| + | == Lift Curve Slope == | ||
| + | |||
[[Image:Naca0012 lift curve slope.JPG]] | [[Image:Naca0012 lift curve slope.JPG]] | ||
<br><br> | <br><br> | ||
The initial slope of the lift curve depends on the Reynold's number. Here I compare the lift curve slope to experimental results.[1] | The initial slope of the lift curve depends on the Reynold's number. Here I compare the lift curve slope to experimental results.[1] | ||
| - | + | <br> | |
== References == | == References == | ||
1. W. J. McCroskey, ''A Critical Assessment of Wind Tunnel Results for the NACA 0012 Airfoil'', NASA Technical Memorandum 10001 9 (1987) <br> | 1. W. J. McCroskey, ''A Critical Assessment of Wind Tunnel Results for the NACA 0012 Airfoil'', NASA Technical Memorandum 10001 9 (1987) <br> | ||
2. L. Lazauskus, [http://http://www.cyberiad.net/library/airfoils/foildata/n0012cl.htm NACA 0012 Lift Data] | 2. L. Lazauskus, [http://http://www.cyberiad.net/library/airfoils/foildata/n0012cl.htm NACA 0012 Lift Data] | ||
Revision as of 18:42, 10 November 2009
Contents |
Introduction
The NACA 0012 airfoil is widely used. The simple geometry and the large amount of wind tunnel data provide an excellent 2D validation case. For this case I use the Spalart-Allmaras turbulence model.
Mesh
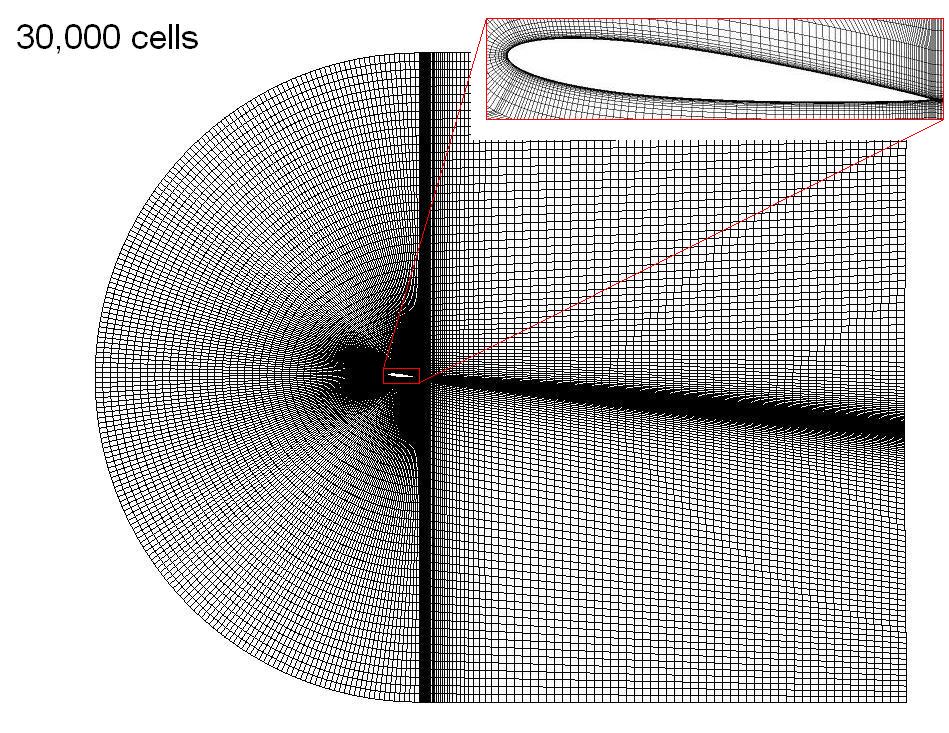
The mesh is a 30,000 cell C-grid. The width off the first cell at the foil boundary is 0.02 mm. At Re = 3e6 this results in a wall y+ = 1.3 ± 0.4 . The mesh shown is for an Angle of Attack of 6 degrees.
Drag Coefficient
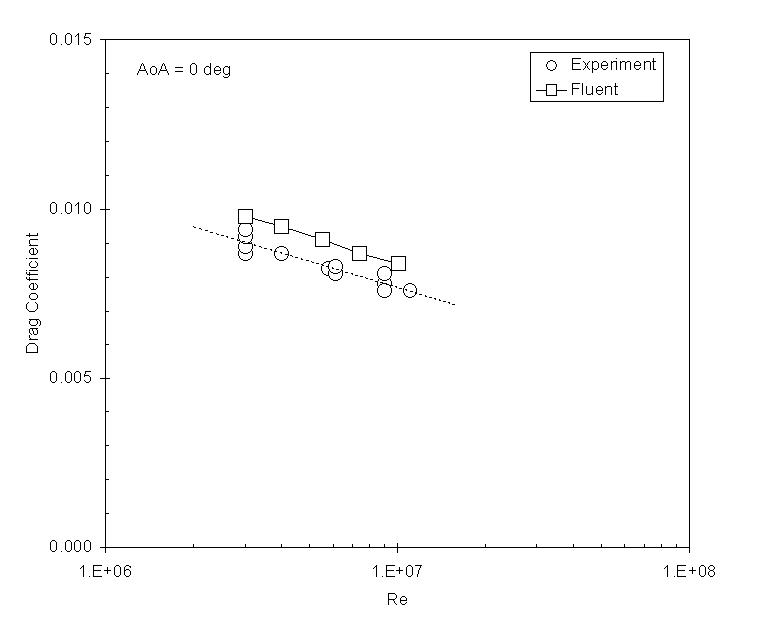
The drag coefficient at zero Angle of Attack depends on the Reynold's number. The experimental data is for an airfoil with a trip wire that forces the experimental boundary layer to be completely turbulent.[1] This corresponds to the Fluent model, which has an active turbulence model over the complete airfoil.
Lift Curve
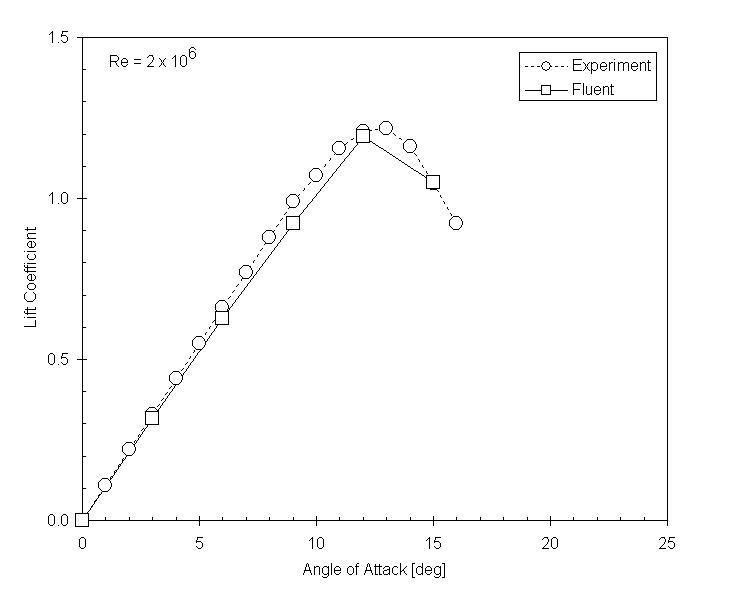
The lift coefficient depends on the Angle of Attack. For Re = 2e6 I compare the lift coefficient to experimental results.[2]
Lift Curve Slope
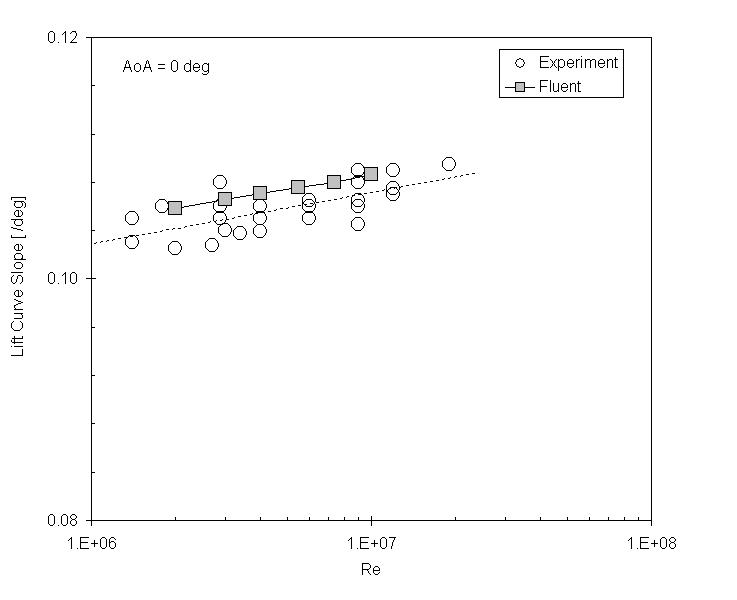
The initial slope of the lift curve depends on the Reynold's number. Here I compare the lift curve slope to experimental results.[1]
References
1. W. J. McCroskey, A Critical Assessment of Wind Tunnel Results for the NACA 0012 Airfoil, NASA Technical Memorandum 10001 9 (1987)
2. L. Lazauskus, NACA 0012 Lift Data
