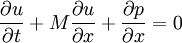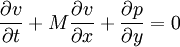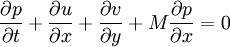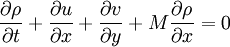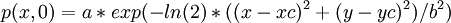2-D linearised Euler equation

Revision as of 07:37, 12 November 2005 by Harish gopalan (Talk | contribs)

Problem Definition

$\frac{\partial u}{\partial t}+M \frac{\partial u}{\partial x}+\frac{\partial p}{\partial x}=0$

$\frac{\partial v}{\partial t}+M \frac{\partial v}{\partial x}+\frac{\partial p}{\partial y}=0$

$\frac{\partial p}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial p}{\partial x}=0$

$\frac{\partial \rho}{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+M\frac{\partial \rho}{\partial x}=0$

where M is the mach number , speed of sound is assumed to be 1, all the variabled refer to acoustic perturbations over the mean flow.

[-50,50]*[-50,50]

$p(x,0)=a*exp(-ln(2)*((x-xc)^2+(y-yc)^2)/b^2)$

Characteristic Boundary Condition

4th Order Compact scheme in space 4th order low storage RK in time

Pressure No mean flow 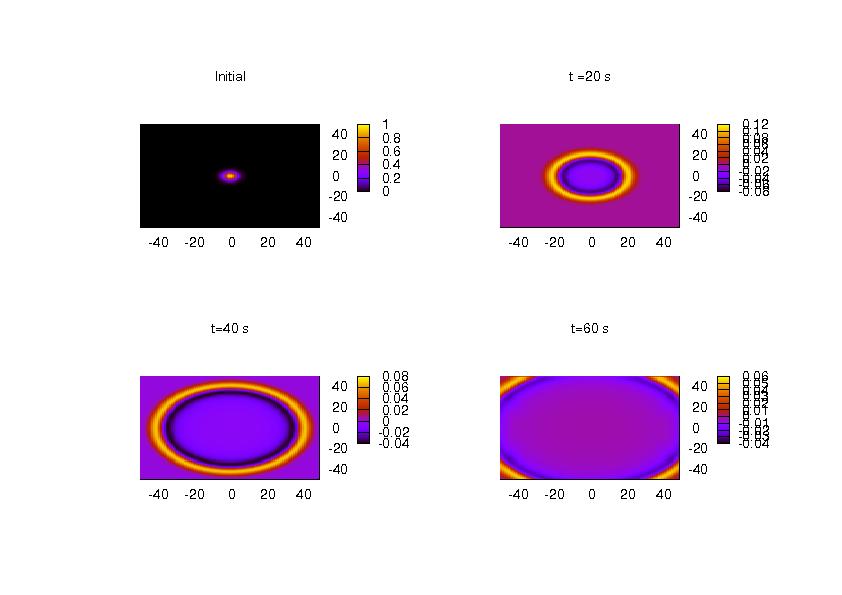Uniform Mean flow to the left at U=0.5 (speed of sound assumed to be 1)

Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.

Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.