Gresho vortex
From CFD-Wiki
Classical Definition
The Gresho vortex was originally designed for incompressible flow, but here we consider the case of Euler equations.
The Gresho problem [1] is a rotating vortex problem independent of time. Angular velocity 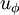 depends only on radius and the centrifugal force is balanced by the gradient of the pressure
depends only on radius and the centrifugal force is balanced by the gradient of the pressure  .
.
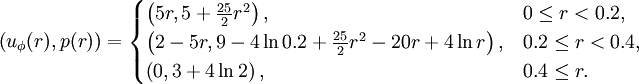
The radial velocity is zero and the density is one everywhere.
Dependence on Mach number
Miczek [2] modified the setup by introducing a reference Mach number. Pressure is scaled such that the rotation acts on this Mach number.
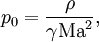
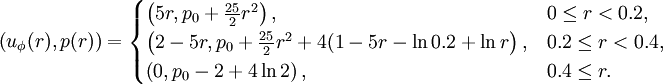
Now, we can use the Gresho vortex as test case how well the numerical scheme performs in dependence of the Mach number.
References
[1] Liska R., Wendroff B. Comparison of Several Difference Schemes on 1D and 2D Test Problems for the Euler Equations. SIAM J. Sci. Comput., 25(3), 995–1017 (23 pages).
[2] Miczek F. Simulation of low Mach number astrophysical flows. München, Technische Universität München, Diss., 2013.
[3] Happenhofer N., Grimm-Strele H., Kupka F., Löw-Baselli B., Muthsam H. A low Mach number solver: Enhancing applicability. Journal of Computational Physics Volume 236, 1 March 2013, Pages 96-118.
[4] Grimm-Strele H., Kupka F., Muthsam H. Curvilinear Grids for WENO Methods in Astrophysical Simulations. Submitted to Computer Physics Communications, 2013.
